第二個Topic講深度學(xué)習(xí),承接前面的《淺談機器學(xué)習(xí)基礎(chǔ)》。
深度學(xué)習(xí)簡介
前面也提到過,機器學(xué)習(xí)的本質(zhì)就是尋找最優(yōu)模型,比如講語音識別,就是將一段語音通過若干模型精準(zhǔn)的轉(zhuǎn)化為對應(yīng)的文字,圖像識別轉(zhuǎn)化為識別結(jié)果,圍棋程序轉(zhuǎn)化為下一步走子,智能對話系統(tǒng)轉(zhuǎn)化為對用戶的回答。
而深度學(xué)習(xí)是機器學(xué)習(xí)的一個大分支,深度學(xué)習(xí)的概念源于對人工神經(jīng)網(wǎng)絡(luò)的研究,深度學(xué)習(xí)的基本結(jié)構(gòu)(也即模型)是深度神經(jīng)網(wǎng)絡(luò)。
講到人工神經(jīng)網(wǎng)絡(luò)就不得不先講感知機,感知機是最簡單的一種人工神經(jīng)網(wǎng)絡(luò),是一種二元線性分類器。感知機抽象于生物神經(jīng)細(xì)胞,神經(jīng)細(xì)胞結(jié)構(gòu)大致可分為:樹突、突觸、細(xì)胞體及軸突。單個神經(jīng)細(xì)胞可被視為一種只有兩種狀態(tài)的機器——激動時為『是』,而未激動時為『否』。神經(jīng)細(xì)胞的狀態(tài)取決于從其它的神經(jīng)細(xì)胞收到的輸入信號量,及突觸的強度(抑制或加強)。當(dāng)信號量總和超過了某個閾值時,細(xì)胞體就會激動,產(chǎn)生電脈沖。電脈沖沿著軸突并通過突觸傳遞到其它神經(jīng)元。為了模擬神經(jīng)細(xì)胞行為,與之對應(yīng)的感知機基礎(chǔ)概念被提出,如權(quán)重(突觸)、偏置(閾值)及激活函數(shù)(細(xì)胞體)。

不同的輸入a與其對應(yīng)的權(quán)重w相乘后全部加和,再與偏置值相加后送入激活函數(shù),經(jīng)激活函數(shù)后得到該感知機的輸出。在人工神經(jīng)網(wǎng)絡(luò)中,規(guī)定神經(jīng)元函數(shù)只能對輸入變量(指向它的節(jié)點的值)線性組合后的結(jié)果進行一次非線性變換(激活函數(shù))。這里的激活函數(shù)可以采用Sigmoid函數(shù),前面的《淺談機器學(xué)習(xí)基礎(chǔ)》對其有講述,Sigmoid函數(shù)的輸出值在0到1之間:

感知機也被用來特指單層人工神經(jīng)網(wǎng)絡(luò),以區(qū)別于多層感知機。感知機無法處理線性不可分問題。什么叫線性不可分?舉個例子,二維平面上有兩類點,無法用一條一維直線將其完全分開;N維空間中有兩類點,用N-1維的分隔超平面無法將兩類點完全分開,就叫做線性不可分。
感知機(神經(jīng)元)之間采用不同的連接方式,也就構(gòu)成了不同的網(wǎng)絡(luò)結(jié)構(gòu)。每個神經(jīng)元都擁有自己的權(quán)重值和偏置值。權(quán)重值和偏置值構(gòu)成了這個網(wǎng)絡(luò)的參數(shù)Θ。

給定Θ參數(shù)值可以定義一個神經(jīng)元,也即定義一個函數(shù);再給定網(wǎng)絡(luò)結(jié)構(gòu),就可以定義一個神經(jīng)網(wǎng)絡(luò),也即一組函數(shù)。
深度神經(jīng)網(wǎng)絡(luò)中的深度意味著神經(jīng)網(wǎng)絡(luò)的層數(shù)很多,神經(jīng)網(wǎng)絡(luò)中第一層是輸入層,最后一層是輸出層,中間數(shù)層是隱藏層,每一層都由若干神經(jīng)元構(gòu)成。
我們可以選擇應(yīng)用Softmax層作為輸出層,Softmax層可以將輸出層神經(jīng)元的輸出值進行處理,使其總和為1。這在分類場景,判定屬于哪類的概率最大時,提供了方便,也使得數(shù)據(jù)更容易被理解。
那具體處理問題時到底選多少層?每一層多少個神經(jīng)元?這個只能靠直覺和試錯。
我們已經(jīng)選定了深度學(xué)習(xí)的基本結(jié)構(gòu),也就是深度神經(jīng)網(wǎng)絡(luò),接下來要談的是對神經(jīng)網(wǎng)絡(luò)輸出結(jié)果好壞的量化評估以及如何找到最佳的參數(shù)值。
就拿我們剛才提到過的分類場景來談,具體一些,手寫數(shù)字識別場景,對于一個神經(jīng)網(wǎng)絡(luò),我們給定其一組初始參數(shù)值,然后將手寫數(shù)字以圖片的形式輸入,在輸出層,我們有10個輸出層神經(jīng)元,每個神經(jīng)元的輸出分別代表了判定輸入是數(shù)字0~9的概率,哪個神經(jīng)元的輸出值最大,也即該神經(jīng)網(wǎng)絡(luò)的判定結(jié)果是該神經(jīng)元對應(yīng)的數(shù)字。
但是,在初始參數(shù)條件,一般神經(jīng)網(wǎng)絡(luò)的輸出結(jié)果并不完全正確,我們需要對其參數(shù)進行優(yōu)化,要優(yōu)化參數(shù),首先要度量誤差,誤差來源于預(yù)測結(jié)果與實際結(jié)果的距離,比如對于手寫數(shù)字識別,給定一張寫著『2』的圖片,最理想的輸出是,只有2對應(yīng)的那個神經(jīng)元輸出為1,其它輸出均應(yīng)該為0。我們可以選擇計算每個神經(jīng)元的輸出與理論結(jié)果的誤差,然后將其加和,由此得到了我們對神經(jīng)網(wǎng)絡(luò)的優(yōu)化目標(biāo),也即通過調(diào)整參數(shù)讓整個損失函數(shù)的函數(shù)值最小。
那我們該如何確定最佳參數(shù)值呢?遍歷肯定不行,如果D層,每層N個神經(jīng)元,那復(fù)雜度就是N的D次方。我們終究還是要選擇梯度下降方法,梯度下降方法的原理在《淺談機器學(xué)習(xí)基礎(chǔ)》中有詳細(xì)的原理介紹。
η是學(xué)習(xí)速率,η后面的式子是損失函數(shù)對該參數(shù)變量的偏導(dǎo)數(shù)。
深度學(xué)習(xí)網(wǎng)絡(luò)分類
如前所述,深度學(xué)習(xí)指的是一類廣泛的機器學(xué)習(xí)技術(shù)和架構(gòu),其特點是采用多層的非線性信息處理方法,這種方法在本質(zhì)上是分層的。根據(jù)這些結(jié)構(gòu)和技術(shù)不同的應(yīng)用領(lǐng)域,如合成/生成或識別/分類,我們可以大致把這些結(jié)構(gòu)分為三類:
無監(jiān)督的或生成式學(xué)習(xí)的深度網(wǎng)絡(luò):針對模式分析和合成任務(wù),用于在沒有目標(biāo)類標(biāo)簽信息的情況下捕捉觀測到的或可見數(shù)據(jù)的高階相關(guān)性。各種文獻中的無監(jiān)督特征或表達(dá)學(xué)習(xí)指的就是這一類深度網(wǎng)絡(luò)。當(dāng)用于生成模式時,它也可以用來描述可見數(shù)據(jù)和其相關(guān)分類的聯(lián)合分布概率,此時它具有可以利用的類別標(biāo)簽,而且這些類別標(biāo)簽被看做是可見數(shù)據(jù)的一部分。在后一種情況中,利用貝葉斯準(zhǔn)則可以把生成學(xué)習(xí)網(wǎng)絡(luò)轉(zhuǎn)換為判別式學(xué)習(xí)網(wǎng)絡(luò)。
有監(jiān)督學(xué)習(xí)的深度網(wǎng)絡(luò):直接提供用于模式分類目的的判別能力,它的特點是描述了可見數(shù)據(jù)條件下的后驗分布(條件概率分布)。這種有監(jiān)督的學(xué)習(xí),目標(biāo)類別標(biāo)簽總是以直接或間接形式給出,所以它們也被稱作判別式深度網(wǎng)絡(luò)。
混合深度網(wǎng)絡(luò):目標(biāo)是判別式模型,往往以生成式或無監(jiān)督深度網(wǎng)絡(luò)的結(jié)果作為重要輔助,可以通過更好地優(yōu)化和正則化上個類別中的深度網(wǎng)絡(luò)來實現(xiàn),也可以通過對第一個類別所述的深度生成式或無監(jiān)督深度網(wǎng)絡(luò)的參數(shù)進行估計時,使用判別式準(zhǔn)則來實現(xiàn)。
在其他文獻里,一般將深度機器學(xué)習(xí)技術(shù)分為深度判別式模型(深度神經(jīng)網(wǎng)絡(luò)DNN、遞歸神經(jīng)網(wǎng)絡(luò)RNN、卷積神經(jīng)網(wǎng)絡(luò)CNN等)和生成式/無監(jiān)督模型(受限玻爾茲曼機RBM、深度信念網(wǎng)絡(luò)DBN、深度玻爾茲曼機DBM、正則化的自編碼器等),然而這種二元分類方法忽略了通過深度學(xué)習(xí)研究所獲得的重要觀點,即生成式和無監(jiān)督學(xué)習(xí)如何通過更好地進行正則化與優(yōu)化,來大幅提高DNN和其他深度判別式和監(jiān)督學(xué)習(xí)模型的訓(xùn)練效果。同時,無監(jiān)督學(xué)習(xí)的深度網(wǎng)絡(luò)并不一定必須是概率模型,也不一定能從模型中得到有意義的采樣。深度有監(jiān)督的學(xué)習(xí)模型適合復(fù)雜系統(tǒng)的端到端學(xué)習(xí);而深度無監(jiān)督學(xué)習(xí)模型,尤其是概率生成模型,更容易理解,更容易嵌入領(lǐng)域知識,更容易組合,對不確定性進行處理。
下面先只講無監(jiān)督和生成式學(xué)習(xí)深度網(wǎng)絡(luò)。
無監(jiān)督學(xué)習(xí)是指在學(xué)習(xí)過程中不使用特定任務(wù)的監(jiān)督信息(如目標(biāo)類別標(biāo)簽)。這一類深度網(wǎng)絡(luò)大多可以通過從網(wǎng)絡(luò)中采樣來有效生成樣本,因此是生成式模型,例如RBM、DBN、DBM和廣義除噪自編碼器。然而這一類別中的有些網(wǎng)絡(luò)采樣并不容易,因而本質(zhì)上并不是生成式的,例如稀疏編碼網(wǎng)絡(luò)和原始形式的深度自編碼器。
生成式或無監(jiān)督深度網(wǎng)絡(luò)有多個子類:
一類是各種自編碼器及其堆疊形式,具體的說,在除噪自編碼器中,輸入向量首先被『破壞』,例如,隨機選擇一定比例的輸入并把它們設(shè)為零,或加入高斯噪聲,然后調(diào)整參數(shù),使隱層編碼結(jié)點重構(gòu)出原始的、未損壞的輸入數(shù)據(jù),調(diào)整參數(shù)所使用的準(zhǔn)則包括原始輸入與重建輸入的最小均方誤差和KL散度準(zhǔn)則。將未損壞數(shù)據(jù)進行轉(zhuǎn)換,獲得編碼表示,并將其作為下一層堆疊自編碼器的輸入。
另一類有生成能力的深度無監(jiān)督模型是深度玻爾茲曼機(DBM),DBM包含很多隱變量層,并且同一層變量之間沒有連接。DBM是玻爾茲曼機(BM)的一個特例。當(dāng)DBM的隱層數(shù)為1時,我們就得到了受限玻爾茲曼機(RBM),RBM與DBM一樣,沒有隱層到隱層和顯層到顯層的連接。RBM的主要優(yōu)點是,通過組合許多RBM,把上一層RBM的特征激勵作為下一層的訓(xùn)練數(shù)據(jù),可以高效的對隱層進行學(xué)習(xí),這樣組合也即得到了深度信念網(wǎng)絡(luò)(DBN)。
還有兩類,一種是和積網(wǎng)絡(luò)(SPN),另一種是無監(jiān)督學(xué)習(xí)模式下的RNN。
自編碼器
深度自編碼器是一類特殊的無分類標(biāo)簽的深度神經(jīng)網(wǎng)絡(luò)。其輸出向量與輸入向量同維,常按照輸入向量的某種形式,通過隱層學(xué)習(xí)一個數(shù)據(jù)的表示或?qū)υ紨?shù)據(jù)進行有效編碼。值得注意的是,這種自編碼器是一種不利用類標(biāo)簽的非線性特征提取方法。就方法本身而言,這種特征提取的目的在于保留和獲得更好的信息表示,而不是執(zhí)行分類任務(wù),盡管有時這兩個目標(biāo)是相關(guān)的。
一個典型的自編碼器擁有一個表示原始數(shù)據(jù)或者輸入特征向量的輸入層;一個或多個表示特征轉(zhuǎn)換的隱層;一個跟輸入層匹配、用于信息重構(gòu)的輸出層。當(dāng)隱層數(shù)目大于1時,這個自編碼器就被視為深層結(jié)構(gòu)。隱層的維度可以小于(當(dāng)目標(biāo)是特征壓縮)或大于(當(dāng)目標(biāo)是映射特征匹配更高維的空間)輸入層的維度。
如果我們在自動編碼器的基礎(chǔ)上加上L1的規(guī)則限制(L1主要是約束每一層中的節(jié)點中大部分都要為0,只有少數(shù)不為0,稀疏約束項),我們就可以得到稀疏自動編碼方法。也就是上面提到的特征壓縮,如果隱藏節(jié)點比可視節(jié)點(輸入、輸出)少的話,被迫的降維,自編碼器會自動習(xí)得訓(xùn)練樣本的特征(變化最大,信息量最多的維度),所謂稀疏性,就是對一對輸入,隱藏節(jié)點中被激活的節(jié)點數(shù)(輸出接近1)遠(yuǎn)遠(yuǎn)小于被抑制的節(jié)點數(shù)目(輸出接近0)。那么使神經(jīng)元大部分的時間都是被抑制的限制被稱作稀疏性限制。
另外提一下降噪自編碼器,原理很簡單,降噪自編碼器與自編碼器的區(qū)別在于,降噪自編碼器在原本自編碼器的輸入上加上了噪聲,然后希望通過訓(xùn)練輸出去除噪聲后的原數(shù)據(jù)。
棧式自編碼器是一個由多層稀疏自編碼器組成的神經(jīng)網(wǎng)絡(luò),由于其隱層數(shù)目大于1,所以可被認(rèn)定為是一種深度自編碼器。
在棧式自編碼器中,前一層的自編碼器的輸出作為其后一層自編碼器的輸入。對于一個n層棧式自編碼器的編碼過程就是,按照從前向后的順序執(zhí)行每一層自編碼器的編碼步驟。
假設(shè)我們要訓(xùn)練一個4層的神經(jīng)網(wǎng)絡(luò)模型用于分類任務(wù),網(wǎng)絡(luò)結(jié)構(gòu)如下:
整個過程分為兩個階段,一個是無監(jiān)督預(yù)訓(xùn)練階段(pre-training),另一個是有監(jiān)督微調(diào)階段。預(yù)訓(xùn)練階段實際上就是一層一層的按照原先訓(xùn)練稀疏自編碼器的方法訓(xùn)練每一層的參數(shù)。
在預(yù)訓(xùn)練階段,首先,我們要采用稀疏自編碼網(wǎng)絡(luò),先訓(xùn)練從輸入層到H1層的參數(shù):
訓(xùn)練完畢后,我們?nèi)コ獯a層,只留下從輸入層到隱藏層的編碼階段。
接著我們訓(xùn)練從H1到H2的參數(shù),我們把無標(biāo)簽數(shù)據(jù)的H1層元素的激活值,作為H2層的輸入層,然后再進行自編碼訓(xùn)練:
最后訓(xùn)練完畢后,再去除H2的解碼層,如此重復(fù),可以訓(xùn)練更高層的網(wǎng)絡(luò),這就是逐層貪婪訓(xùn)練的思想。
訓(xùn)練完H2之后,我們就可以接分類層softmax,用于多分類任務(wù):
以上的過程就是所謂的無監(jiān)督預(yù)訓(xùn)練。后面接著就是利用上面的參數(shù)作為網(wǎng)絡(luò)的初始值,繼續(xù)進行神經(jīng)網(wǎng)絡(luò)的訓(xùn)練了。
玻爾茲曼機
首先是玻爾茲曼分布,其分布的概率公式如下:

pi為量子態(tài)i的幾率,εi為量子態(tài)i的能量,k為玻爾茲曼常數(shù),T為系統(tǒng)溫度,M為系統(tǒng)可具有的量子態(tài)的總數(shù)。
可以看到,εi越大,pi越小,也即物理意義為,在保守力場作用下,低能量的狀態(tài)比高能量的狀態(tài)擁有更高的分布幾率,舉個例子,一個大盒子里放有若干個球,球總是傾向于先占據(jù)盒子的底部,即重力勢能低的位置,也即處于穩(wěn)態(tài)。
然后是BM,BM是玻爾茲曼機,玻爾茲曼機是一種隨機神經(jīng)網(wǎng)絡(luò)(同時也是遞歸神經(jīng)網(wǎng)絡(luò)),描述一個隨機網(wǎng)絡(luò)主要需要確定兩點。
第一個是這個隨機網(wǎng)絡(luò)的概率分布函數(shù),由于網(wǎng)絡(luò)節(jié)點的取值狀態(tài)是隨機的,從貝葉斯網(wǎng)絡(luò)的觀點來看,要描述整個網(wǎng)絡(luò),需要三種概率分布,分別是聯(lián)合概率分布、邊緣概率分布(邊緣概率分布的邊緣源于它是一組概率的加和,通常被放在表的邊緣,P(A)=sum(P(B)*P(A|B)+P(C)*P(A|C)))和條件概率分布。
第二個是這個隨機網(wǎng)絡(luò)的能量函數(shù),隨機神經(jīng)網(wǎng)絡(luò)根植于統(tǒng)計力學(xué),受統(tǒng)計力學(xué)的啟發(fā),引入了能量函數(shù)。能量函數(shù)是描述整個系統(tǒng)狀態(tài)的一種測度,系統(tǒng)越有序或概率分布越集中,系統(tǒng)的能量越小。反之,系統(tǒng)越無序或者概率分布越趨向于均勻分布,則系統(tǒng)的能量越大(與前面講過的熵類似)。能量函數(shù)的最小值,也就對應(yīng)了系統(tǒng)的穩(wěn)態(tài),一般情況下,我們就是要找到系統(tǒng)的穩(wěn)態(tài),也就是能量函數(shù)的最小值。
沒有特定限制連接方式的玻爾茲曼機目前為止并沒有在機器學(xué)習(xí)的實際問題中起到什么作用,只是理論上顯得有趣。
接下來是受限玻爾茲曼機,圖示如下:
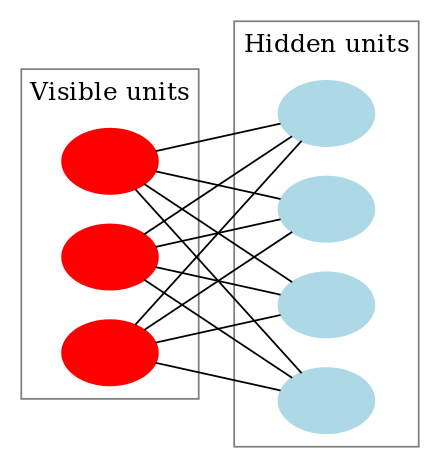
RBM與前饋神經(jīng)網(wǎng)絡(luò)不一樣,RBM在可見層和隱層間的連接方向是不確定的,值可以進行雙向傳播;且可見層與隱層,層間完全連接,而層內(nèi)沒有連接,也即二分圖(不受限玻爾茲曼機隱層單元間存在連接,使之成為遞歸神經(jīng)網(wǎng)絡(luò))。
標(biāo)準(zhǔn)的受限玻爾茲曼機由二值(布爾/伯努利)隱層和可見層單元組成,權(quán)重矩陣W中的每個元素指定了隱層單元hj和可見層單元vi之間連接的權(quán)重值(受限玻爾茲曼機每條邊必須連接一個隱單元和可見單元),此外對于每個可見層單元vi有偏置ai,對每個隱層單元hj有偏置bi。前面在講述玻爾茲曼機時提到過,我們要確定兩部分內(nèi)容,一個是聯(lián)合概率分布、邊緣概率分布和條件概率分布,另一個是能量函數(shù)。給出了前面的定義,我們先給出受限玻爾茲曼機的能量函數(shù):

更換其為矩陣表示:

根據(jù)能量函數(shù),我們進一步給出受限玻爾茲曼機中隱層和可見層之間的聯(lián)合概率分布:

邊緣概率分布(通過對所有隱層配置求和得到):

由于受限玻爾茲曼機是一個二分圖,所以隱層單元的激活在給定可見單元取值的情況下是條件獨立的,所以條件概率分布:


單個節(jié)點的激活概率為:

和:

σ為Sigmoid函數(shù)。
上面的過程是不是與我們在《淺談機器學(xué)習(xí)基礎(chǔ)》文中推導(dǎo)LR目標(biāo)函數(shù)的過程有些相似?先利用Sigmoid函數(shù)表示出每個節(jié)點的激活概率,接下來最大化訓(xùn)練集V的生成概率,訓(xùn)練RBM也是同理:

訓(xùn)練受限玻爾茲曼機,即最優(yōu)化權(quán)重矩陣W,使訓(xùn)練集V的生成概率最大,常采用的算法叫做對比分歧(contrastive divergence,CD)算法。這一算法在梯度下降的過程中使用吉布斯采樣完成對權(quán)重的更新,與訓(xùn)練前饋神經(jīng)網(wǎng)絡(luò)中利用反向傳播算法(BP)類似。
首先簡單說一下什么是吉布斯采樣(Gibbs),當(dāng)積分、期望、聯(lián)合概率分布很難計算出來(NP問題)的時候,我們利用條件概率產(chǎn)生符合分布的樣本,用于估計分布的期望,邊緣分布;是一種在無法精確計算情況下,用計算機模擬的方法。
之后是CD-k算法,CD算法的大概思路是,從任意一個樣本開始,用經(jīng)過k次吉布斯采樣得到的樣本來近似梯度的計算,然后依照梯度去更新參數(shù),與前面講過的梯度上升/下降算法原理相同。
CD-k算法的具體過程借用別人文章中的截圖來描述:
對所有的樣本都進行k次吉布斯采樣,圖中藍(lán)色的兩個sample函數(shù),就是進行吉布斯采樣的過程,sample_h_given_v(v,W,a,b)做的事情是這樣的(sample_v_given_v(h,W,a,b)類似):
記qj=P(hj|v),j=1,2,…,nh,產(chǎn)生一個[0,1]的隨機數(shù)rj,對每一個hj,如果rj<qj,則hj=1,否則hj=0。也即qj這個條件概率越大,越接近1,那hj為1的概率就越大,也即根據(jù)條件概率進行吉布斯采樣。
整個RBM的訓(xùn)練過程如下:
然后是DBN,DBN也即深度信念網(wǎng)絡(luò),深度信念網(wǎng)絡(luò)可使用多個RBM堆疊而成,并可使用梯度下降法和反向傳播算法(BP)進行調(diào)優(yōu)(使用BP對整個DBN微調(diào),對RBM的無監(jiān)督預(yù)訓(xùn)練獨立用CD算法)。
具體的說,在講自動編碼器的時候,我們舉了一個逐層貪婪預(yù)訓(xùn)練方法的例子,這種無監(jiān)督逐層預(yù)訓(xùn)練是一種通用技術(shù),也就是說,不僅前面的自編碼器可以逐層預(yù)訓(xùn)練,RBM堆疊起來的DBN也可以進行無監(jiān)督的逐層預(yù)訓(xùn)練,方法與自編碼器的訓(xùn)練過程類似,主要分為如下兩步:
第一步:分別單獨無監(jiān)督的訓(xùn)練每一層RBM網(wǎng)絡(luò),確保特征向量映射到不同特征空間時,都盡可能多地保留特征信息。
舉個例子,隱含層RBM H可以看做是RBM H+1的可見層。第一個RBM的輸入層即是整個網(wǎng)絡(luò)的輸入層,逐層貪婪預(yù)訓(xùn)練的工作模式如下:
- 通過CD算法對所用訓(xùn)練樣本訓(xùn)練第一個RBM
- 將第一個RBM的隱含層作為第二個RBM的輸入層數(shù)據(jù)進行訓(xùn)練,同樣采用CD算法
- 對所有層重復(fù)上面的過程
- 和棧式自編碼器一樣,通過預(yù)訓(xùn)練后,網(wǎng)絡(luò)堆疊一個或多個層間全連接的RBM隱含層進行擴展,這構(gòu)成了一個可以通過反向傳播進行微調(diào)的多層感知機。
第二步:在DBN的最后一層設(shè)置BP網(wǎng)絡(luò),接受RBM的輸出特征向量作為它的輸入特征向量,有監(jiān)督地訓(xùn)練實體關(guān)系分類器。每一層RBM網(wǎng)絡(luò)只能確保自身層內(nèi)權(quán)值對該層特征向量映射達(dá)到最優(yōu),并不是對整個DBN的特征向量映射達(dá)到最優(yōu),所以反向傳播網(wǎng)絡(luò)還將錯誤信息自頂向下傳播至每一層RBM,微調(diào)整個DBN網(wǎng)絡(luò)。
每次訓(xùn)練都使當(dāng)前RBM隱層激活概率無限接近于可見層,實際上,這樣的貪婪過程達(dá)到了近似的最大似然學(xué)習(xí),而且這個學(xué)習(xí)過程不需要標(biāo)簽信息,用的是可見層輸入作為調(diào)整依據(jù),所以是無監(jiān)督的。
RBM網(wǎng)絡(luò)訓(xùn)練模型的過程可以看做對一個深層BP網(wǎng)絡(luò)權(quán)值參數(shù)的初始化,使DBN克服BP網(wǎng)絡(luò)因隨機初始化權(quán)值參數(shù)而容易陷入局部最優(yōu)和訓(xùn)練時間過長的問題點。
上述訓(xùn)練DBN的過程,第一步叫做預(yù)訓(xùn)練,第二步叫做微調(diào)。最上面有監(jiān)督學(xué)習(xí)的那一層,根據(jù)具體的應(yīng)用可以換成任何分類器模型,不必是BP網(wǎng)絡(luò)。
這個過程和棧式自編碼器很相似,只是用RBM將自編碼器進行替換,用CD算法訓(xùn)練RBM替代BP算法訓(xùn)練自編碼器。
這里再提一下反向傳播算法。
反向傳播(英語:Backpropagation,縮寫為BP)是“誤差反向傳播”的簡稱,是一種與最優(yōu)化方法(如梯度下降法)結(jié)合使用的,用來訓(xùn)練人工神經(jīng)網(wǎng)絡(luò)的常見方法。
BP算法主要分為兩個階段:
第一個階段是激勵傳播:每次迭代中的傳播環(huán)節(jié)也分為兩步:1.(前向傳播階段)將訓(xùn)練送入網(wǎng)絡(luò)以獲得激勵響應(yīng)。2.(反向傳播階段)將激勵響應(yīng)與訓(xùn)練輸入對應(yīng)的目標(biāo)輸出求差,從而獲得隱層和輸出層的響應(yīng)誤差。
第二個階段是權(quán)重更新:對于每個突觸上的權(quán)重,更新步驟也有兩步(參見上篇文章當(dāng)中對梯度下降算法的講述):1.得到對應(yīng)的梯度。2.用當(dāng)前權(quán)重減去梯度。

BP算法實際上就是應(yīng)用在多層網(wǎng)絡(luò)中的梯度下降算法,原理與梯度下降算法相同,但區(qū)別在于BP算法需要求不同層連接所對應(yīng)的梯度,而不是像普通的梯度下降算法那樣,只需處理一層的問題。
利用BP算法計算輸出層連接的梯度時,過程與普通梯度下降算法相同;但如果j是網(wǎng)絡(luò)中任一內(nèi)層神經(jīng)元,求損失函數(shù)E對于相應(yīng)連接權(quán)重wij(i是j下一層的神經(jīng)元,wij即兩者之間連接的權(quán)重)的偏導(dǎo)數(shù)就不太容易了,需要先求對oj的偏導(dǎo)。
考慮E為接受來自神經(jīng)元j輸入的所有神經(jīng)元L = u,v,...,w輸入的函數(shù):

對oj取全微分,可以得到該導(dǎo)數(shù)的一個遞歸表達(dá)式:

也即,只要知道所有下一層(指離輸出層更近的一層)的輸出ol的導(dǎo)數(shù),即可計算oj的導(dǎo)數(shù),把它們放在一起:

其中:

所以得到BP算法的權(quán)重迭代公式(與普通梯度下降法參數(shù)迭代公式形式類似):

以上即為BP算法推導(dǎo)的全過程。
BP算法說到底是種梯度下降算法,前面也提到過,梯度下降法能得到局部最優(yōu),但并不能保證一定會得到全局最優(yōu)。我們通常采用RBM pre-train的方法來避免其收斂到局部最小值。
根據(jù)前面的內(nèi)容,好像稀疏自動編碼器(sparse autoencoder)堆疊得到棧式自動編碼器(stacked autoencoders),RBM堆疊得到DBN;而且二者都可以被用來做有監(jiān)督DNN的預(yù)訓(xùn)練,用的還都是同樣的無監(jiān)督逐層預(yù)訓(xùn)練方法,二者實際上也都是起到了特征探測器的作用,都是給定一個輸入,得到一個中間層,并利用中間層去重構(gòu)一個和輸入相同的樣本,然后利用不同的評價指標(biāo),通過某種優(yōu)化方法,盡可能的縮小輸出樣本和輸入樣本之間的差異。那它們的區(qū)別在什么地方呢?
首先Autocoder是一個確定模型,它的輸入和輸出之間有著嚴(yán)格的數(shù)學(xué)公式;而RBM源于BM,源于玻爾茲曼分布,是一個基于概率的不確定模型。
Autocoder訓(xùn)練時采用BP算法,直接做梯度下降(看成只有一層的BP神經(jīng)網(wǎng)絡(luò)),而RBM采用CD-k算法,只能利用k次吉布斯采樣的結(jié)果去近似的計算梯度。
深度神經(jīng)網(wǎng)絡(luò)的訓(xùn)練
一般對DNN的訓(xùn)練要從兩個角度去考慮,第一個是如何讓網(wǎng)絡(luò)在訓(xùn)練集上有良好的表現(xiàn),第二個是如何在訓(xùn)練集表現(xiàn)良好的前提下,使其在測試集上也有同樣的表現(xiàn)。
如何在訓(xùn)練集上調(diào)優(yōu)
選擇合適的損失函數(shù)
前面我們默認(rèn)采用的都是平方誤差損失函數(shù),但很多時候,平方誤差損失函數(shù)并不是我們最好的選擇,比如當(dāng)我們用Softmax作為輸出層時,就更傾向于選擇交叉熵?fù)p失函數(shù)。

前面我們也提到過熵的定義,知道熵是一個不確定性的測度,也就是說,我們對于某件事情知道得越多,那么,熵就越小,因而對于試驗的結(jié)果我們越不感到意外。交叉熵的概念就是用來衡量估計模型與真實概率分布之間的差異情況的。

其中y為期望的輸出,a為神經(jīng)元實際的輸出(a=σ(z), where z=∑Wj*Xj+b)。
與方差誤差函數(shù)一樣,交叉熵函數(shù)同樣擁有兩個性質(zhì),一個是非負(fù)性,一個是當(dāng)真實輸出a與期望輸出y接近時,損失函數(shù)的函數(shù)值接近于0。
另外,它可以克服方差代價函數(shù)更新權(quán)重過慢的問題。我們看看它的導(dǎo)數(shù):


從式子中我們可以看到,權(quán)重的更新是受σ(z)?y這一項影響,也即誤差越大,權(quán)重更新速度越快,誤差越小,更新速度越慢。這項性質(zhì)在上面的交叉熵?fù)p失函數(shù)曲面圖中也可以體現(xiàn)出來,誤差越大,曲面越陡峭,偏導(dǎo)也就越大,梯度下降也就越快。
Mini-batch
我們上篇文章《淺談機器學(xué)習(xí)基礎(chǔ)》中,講過梯度下降算法(batch-GD),講過隨機梯度下降算法(SGD),它們的區(qū)別在于,batch-GD單次迭代要使用整個訓(xùn)練集,而SGD單次迭代每次只使用單個樣本。那我們就一定要走兩個極端嗎,要么全部使用,要么只使用一個?我們可以選擇只使用一部分,把整個訓(xùn)練集拆成一部分一部分使用,這就叫做mini-batch,我們可以把SGD看做mini-batch的特例,也即batch size = 1,而batch-GD的batch size就等于整個訓(xùn)練集。
而且還要引入一個epoch的概念,一次參數(shù)更新叫做一次迭代,當(dāng)經(jīng)歷若干次迭代后,全部訓(xùn)練樣本都已經(jīng)被使用過了,這就叫一個epoch。batch-GD一次迭代就是一個epoch,SGD要迭代訓(xùn)練樣本數(shù)目次,才算是一個epoch。

對于batch-GD,每次迭代的梯度方向計算由所有訓(xùn)練樣本共同投票決定,計算損失函數(shù)在整個訓(xùn)練集上的梯度方向,沿著該方向搜尋下一個迭代點。”batch“的含義是訓(xùn)練集中所有樣本參與每一輪迭代。
batch GD每一輪迭代需要所有樣本參與,對于大規(guī)模的機器學(xué)習(xí)應(yīng)用,經(jīng)常有billion級別的訓(xùn)練集,計算復(fù)雜度非常高。因此,有學(xué)者就提出,反正訓(xùn)練集只是數(shù)據(jù)分布的一個采樣集合,我們能不能在每次迭代只利用部分訓(xùn)練集樣本呢?這就是mini-batch算法。
假設(shè)訓(xùn)練集有m個樣本,每個mini-batch(訓(xùn)練集的一個子集)有b個樣本,那么,整個訓(xùn)練集可以分成m/b個mini-batch。
SGD就是mini-batch的一個特殊情況,batch size = 1。
然后是Online GD,隨著互聯(lián)網(wǎng)行業(yè)的蓬勃發(fā)展,數(shù)據(jù)變得越來越“廉價”。很多應(yīng)用有實時的,不間斷的訓(xùn)練數(shù)據(jù)產(chǎn)生。在線學(xué)習(xí)(Online Learning)算法就是充分利用實時數(shù)據(jù)的一個訓(xùn)練算法。
Online GD于mini-batch GD/SGD的區(qū)別在于,所有訓(xùn)練數(shù)據(jù)只用一次,然后丟棄。這樣做的好處是可以最終模型的變化趨勢。比如搜索廣告的點擊率(CTR)預(yù)估模型,網(wǎng)民的點擊行為會隨著時間改變。用batch算法(每天更新一次)一方面耗時較長(需要對所有歷史數(shù)據(jù)重新訓(xùn)練);另一方面,無法及時反饋用戶的點擊行為遷移。而Online Leaning的算法可以實時的最終網(wǎng)民的點擊行為遷移。
選擇新的激活函數(shù)
這里要先提一個問題,就是神經(jīng)網(wǎng)絡(luò)并不一定是層數(shù)越多,越深越好,層數(shù)多了也會隨之產(chǎn)生很多問題,比如梯度消失和梯度爆炸。
先簡單的說一下梯度消失現(xiàn)象,因為前面也講過BP算法,我們知道,梯度的傳播是反向的,從輸出層向輸入層,如果層數(shù)過多,就會導(dǎo)致這樣的問題,越靠近輸出層的層梯度越大,學(xué)習(xí)的也越快,而越靠輸入層,梯度就越小,參數(shù)更新也就越慢,如果整個網(wǎng)絡(luò)的層數(shù)又多,會導(dǎo)致輸入層附近的層幾乎無法有效更新,梯度幾乎為零,這就叫梯度消失。
但是梯度消失的本質(zhì)是什么?我們前面講過BP算法的推導(dǎo):

其中:

可以看到,除了輸出層,計算每一層的梯度都是要乘以上一層梯度的一部分以及層間連接的權(quán)重和的,而計算上一層的梯度這部分又要乘以上上層梯度的一部分,是個連乘式,所以層數(shù)越多,就是越多的數(shù)相乘,如果這些數(shù)字都小于1,那么乘的越多,越接近輸入層,算出來的梯度就越接近零,如果這些數(shù)字都大于1,那么乘的越多,越接近輸入層,算出來的梯度就越大。梯度接近零叫做梯度消失,梯度變得過大就叫做梯度爆炸,而且我們發(fā)現(xiàn)這個乘數(shù)是個累加項,而且這個累加項里面,包含權(quán)重wjl,所以如果初始權(quán)重過小,那梯度消失的風(fēng)險就大,如果初始權(quán)重過大,那就很可能會梯度爆炸,唯一可能的情況是讓這些乘積基本等于1,但這不太可能。
那我們怎么解決這個梯度消失的問題呢?看資料里面講,從2006年起,我們通過前面講過的RBM pre-train來解決梯度消失的問題,畢竟RBM pre-train靠的是無監(jiān)督逐層訓(xùn)練,是種最大似然學(xué)習(xí),最后的有監(jiān)督BP,只是用來微調(diào)的。但是2015年之后,人們一般采用ReLU激活函數(shù)來避免梯度消失/爆炸的問題。
Rectified Linear Unit (修正線性單元/線性整流函數(shù),ReLU),函數(shù)圖像如下:

我們將其與其他常見的Sigmoid激活函數(shù)圖像作對比:

ReLU函數(shù)的表現(xiàn)通常優(yōu)于其他激活函數(shù),廣泛使用于諸如圖像識別等計算機視覺人工智能領(lǐng)域,其具有如下幾個優(yōu)點:
- 計算速度快,因為其由兩段線性函數(shù)構(gòu)成,計算起來不知道比Sigmoid快到哪里去
- ReLU有一定仿生物學(xué)原理,ReLU激活函數(shù)與人腦中神經(jīng)元的激活方式最為類似,人腦接受相應(yīng)刺激后,只有少量相關(guān)神經(jīng)元(1%-4%)被激活,而大多數(shù)神經(jīng)元都處于被抑制的狀態(tài),Sigmoid函數(shù)在輸入為0時就已經(jīng)是1/2半飽和的穩(wěn)定狀態(tài)了,不夠符合實際生物學(xué)對人工神經(jīng)網(wǎng)絡(luò)的期望,而ReLU的表現(xiàn)要好的多,不過一般情況下,使用了ReLU,網(wǎng)絡(luò)中也大概有50%的神經(jīng)元會處于激活狀態(tài)。
- 采用ReLU可以解決梯度消失/爆炸的問題,前面講過梯度消失/爆炸的原理,在于復(fù)雜多層網(wǎng)絡(luò)下的梯度連乘,而ReLU的價值就在于抑制相當(dāng)一部分神經(jīng)元的激活,實際上是對網(wǎng)絡(luò)進行了簡化,去掉了網(wǎng)絡(luò)中被抑制的那些神經(jīng)元。
ReLU函數(shù)還有幾種變體,往往是更改了輸入小于0時的函數(shù)曲線,比如Leaky ReLU、Parametric ReLU等,不詳述。
另外還要說的一點就是Maxout,ReLU其實是Maxout的一種特例。
那什么是Maxout?

我們知道,在人工神經(jīng)網(wǎng)絡(luò)中,規(guī)定神經(jīng)元函數(shù)只能對輸入變量線性組合后的結(jié)果進行一次非線性變換。而這次非線性變換,就是激活函數(shù)。
接下來具體講一下Maxout的算法流程,首先對于每個隱藏層神經(jīng)元,如果它接受d個輸入,那么Maxout隱藏層每個神經(jīng)元的計算公式如下:
上面的公式就是maxout隱藏層神經(jīng)元i的計算公式。其中,k就是maxout層所需要的參數(shù)了,由我們?nèi)藶樵O(shè)定大小。公式中Z的計算公式為:
權(quán)重W是一個大小為(d,m,k)三維矩陣,b是一個大小為(m,k)的二維矩陣,這兩個就是我們需要學(xué)習(xí)的參數(shù)。而這個k就是我們同時訓(xùn)練的參數(shù)組數(shù)。本來傳統(tǒng)的人工神經(jīng)網(wǎng)絡(luò),第i層到第i+1層只有一組參數(shù)(k=1),但是現(xiàn)在,我們同時訓(xùn)練k組參數(shù),然后選擇激活值最大的作為輸出。
以前的做法是,z=W*X+b,然后out=f(z),f就是我們通常講的激活函數(shù),比如Sigmoid、tanh。
而在Maxout里面,相當(dāng)于在每個輸出神經(jīng)元前面又加了一層,相當(dāng)于對輸入變量線性組合后的結(jié)果并不直接送到輸出神經(jīng)元里面,而是相當(dāng)于新加了一個『隱隱層』,這個『隱隱層』有k個神經(jīng)元,這個k就是Maxout里面的那個參數(shù)k,然后前面線性組合的結(jié)果就分別送到這k個神經(jīng)元里面,分別進行計算(比如k等于5):
z1=w1*x+b1
z2=w2*x+b2
z3=w3*x+b3
z4=w4*x+b4
z5=w5*x+b5
然后取最大的out=max(z1,z2,z3,z4,z5)作為輸出,同時訓(xùn)練k組參數(shù),這就是Maxout。
Maxout激活函數(shù)的圖像如下:

我們可以看到k=2時第一個圖像就是ReLU的函數(shù)圖像。按我的理解,ReLU就是Maxout的k=2,然后在隱隱層放了一個z=0的神經(jīng)元。
自適應(yīng)學(xué)習(xí)速率
上篇文章講梯度下降時提到過學(xué)習(xí)速率η,它對訓(xùn)練效果也起到很重要的影響,如果η過大,那每次更新后,總誤差可能并不會縮小;而如果η過小,那訓(xùn)練速度又會變得相當(dāng)慢。所以我們很自然的有這樣的想法,學(xué)習(xí)速率η不應(yīng)該是一直不變的,我們希望這個學(xué)習(xí)速率η能夠隨著每次epoch而減小。
Adagrad就是針對這一問題提出的,自適應(yīng)地為各個參數(shù)分配不同學(xué)習(xí)率的算法。其公式如下:

學(xué)習(xí)速率η不再恒定不變,而是根據(jù)上式持續(xù)更新,下面的分母會隨著迭代次數(shù)的增加累加gi,gi是第i次更新所得到偏導(dǎo)數(shù)。
也即,對于所有的參數(shù)來講,學(xué)習(xí)速率都是越來越小的。而且,偏導(dǎo)越小,學(xué)習(xí)速率減小的就越慢。
第一條很好理解,第二條要簡單解釋一下,如果偏導(dǎo)很小,說明本來的更新速率就很小,如果再將學(xué)習(xí)速率這個參數(shù)以一個較快的速度減小,那這個維度下的總參數(shù)更新速率就會變的過慢。
當(dāng)然Adagrad也不是唯一的算法,擁有類似功能的還有RMSprop、Adadelta、AdaSecant、Adam等,而且一般而言Adam是目前的最優(yōu)選擇。
Momentum
我們考慮這樣一個問題,如果單純的只靠梯度來作為權(quán)重更新的唯一依據(jù),會出現(xiàn)什么樣的問題,如下圖所示:

當(dāng)梯度非常小,也即曲面在對應(yīng)維度上非常平緩時,權(quán)重的更新會變得相當(dāng)慢;在鞍點,也即偏導(dǎo)數(shù)為0的點,該維度權(quán)重會停止更新;而且也很容易停留在局部最小值而達(dá)不到全局最小值。
Momentum是沖量的意思,不過我們可以簡單的把它理解為慣性,把梯度下降看做一個小球沿曲線滑落的過程,這樣即便在梯度為零的點,也能以一個較快的速度進行梯度下降,甚至還有可能幫助損失函數(shù)突破局部最小值的限制,到達(dá)全局最小值。
前面所提到的表現(xiàn)優(yōu)秀的Adam算法,就相當(dāng)于RMSProp (高級版Adagrad) + Momentum。
如何優(yōu)化在測試集上的表現(xiàn)
模型由于采用了過于復(fù)雜的參數(shù),從而在訓(xùn)練集上擁有良好表現(xiàn),而在測試集上表現(xiàn)很差,這樣的現(xiàn)象叫做過擬合。這一部分就是要講如何解決過擬合的問題。
增大訓(xùn)練集
首先來講最簡單的一個方法,增大訓(xùn)練集,通過使用更大的訓(xùn)練集來增強模型對于各種樣本的適應(yīng)性。
增大訓(xùn)練集也有兩種方法,一個自然是去找到更多的訓(xùn)練樣本,而另一個,是去創(chuàng)造更多的訓(xùn)練樣本。比如在圖像識別中,我們可以通過對已有圖像訓(xùn)練樣本的角度進行調(diào)整來創(chuàng)造一個新的訓(xùn)練樣本,我們也可以通過在訓(xùn)練樣本中加上一些噪聲來創(chuàng)造新的訓(xùn)練樣本等。
提早停止(Early Stopping)

模型在測試集上的誤差往往首先會隨著測試集誤差的減小而減小,但到了后期,模型就會傾向于通過過擬合來進一步降低自身在訓(xùn)練集上的誤差,而這樣的優(yōu)化實際上是升高了模型在測試集上的誤差的。所以我們可以通過提前停止訓(xùn)練來一定程度上避免過擬合。
正則化
正則化的目的是為了防止過擬合,但是正則化為什么可以防止過擬合?
正則化是在我們通常的損失函數(shù)后面加一個正則項,這個正則項實際上是一個對參數(shù)大小的懲罰項,那為什么正則項可以限制參數(shù)不能過大?
因為正則項里面通常包含參數(shù),而我們的優(yōu)化目的又是盡可能的縮小損失函數(shù)函數(shù)值,所以在優(yōu)化的過程中,我們就會讓參數(shù)盡可能的小。那為什么參數(shù)小了就可以防止過擬合?我讀的資料里面寫的都是參數(shù)越大,模型越復(fù)雜,越容易過擬合,那為什么參數(shù)大了模型就越復(fù)雜?
我們可以想一下,模型函數(shù)求導(dǎo)后的式子中是會保留有參數(shù)的,如果參數(shù)越大,也就意味著模型的導(dǎo)數(shù)越大,也就意味著模型曲線越不平滑,也就越容易通過各種扭曲去擬合噪聲樣本點,也即越容易發(fā)生過擬合。
L0,L1,L2正則項是機器學(xué)習(xí)中常用的正則項:
L0:指非零參數(shù)的個數(shù)。前面講過正則項的目的是為了懲罰參數(shù)過大,在這里也就是希望零參數(shù)越多越好,非零參數(shù)越少越好;優(yōu)化損失函數(shù)正好是限制了正則項過大,也即限制了非零參數(shù)的個數(shù)過多。但使用L0正則項有個問題,就是難以優(yōu)化,所以一般不用。
L1:

L2:

對于使用了L1、L2正則項的損失函數(shù)來說,往極小值處優(yōu)化自身函數(shù)值實際上就限制了正則項不能過大,也就限制了w不能過大,也即防止了過擬合。
L1會趨向于產(chǎn)生少量的特征,而其他的特征都是0,也即實現(xiàn)稀疏,只保留少量特征。而L2會選擇更多的特征,這些特征都會接近于0。L2正則項也叫權(quán)重衰減,是最常用的正則項,而且?guī)2的回歸,就是我們上篇文章所提到過的嶺回歸,上篇文章說『嶺回歸就是在原來最小二乘法式子求逆之前先加上一個階數(shù)與樣本數(shù)相同的對角矩陣,也即加上一個正則項,使矩陣為奇異的風(fēng)險大降低,損失了無偏性,來換取高的數(shù)值穩(wěn)定性』,里面的這個正則項,就可以理解為L2正則項。
Dropout
Dropout也是防止過擬合的一種方法。基本原理很簡單,就是訓(xùn)練時,每次更新參數(shù)之前,隨機去掉網(wǎng)絡(luò)中p%的神經(jīng)元,也即更改了網(wǎng)絡(luò)結(jié)構(gòu),讓整個網(wǎng)絡(luò)變得更簡單。如果與前面的梯度下降結(jié)合起來,那就是每次使用訓(xùn)練集的一個新的mini-batch之前,都隨機丟掉網(wǎng)絡(luò)中p%的神經(jīng)元,用剩下的神經(jīng)元進行訓(xùn)練,進行參數(shù)更新。
然后到使用測試集的時候,使用完整的網(wǎng)絡(luò),但所有權(quán)重統(tǒng)一乘以(1-p)%。因為訓(xùn)練時只用部分神經(jīng)元就生成了較為合適的輸出z,如果使用了全部的神經(jīng)元而權(quán)重仍然使用訓(xùn)練時的權(quán)重,那結(jié)果可能就會變成z的n倍。
而且因為前面講了是隨機去掉網(wǎng)絡(luò)中p%的神經(jīng)元的,所以可能若干次訓(xùn)練的神經(jīng)網(wǎng)絡(luò)是會共享部分神經(jīng)元的,當(dāng)然也可能不共享,如果p較大的話。
如果非要講原理的話,我借用我在其他資料里面看到的,當(dāng)一群人組隊做事情的時候,如果每個人都想著,我的隊友會干活的,那什么事情都完成不了;如果每個人都認(rèn)為,我的隊友不行,還是得靠我自己,那么事情會做的好的多:>
Network Structure
有些神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)天然就是能防止過擬合的,比如CNN,池化過程避免了過擬合。
