前面一篇文章貝葉斯統(tǒng)計:初學指南介紹了最簡單的 Metropolis 采樣方法,本文將介紹另一種采樣 Metropolis-Hastings ,并且會對前文介紹的例子給出證明,為什么 Metropolis 采樣work。
回顧
我們簡單的回顧下前文的內(nèi)容,我們首先介紹了為什么需要有mcmc,假設有一個貝葉斯公式:
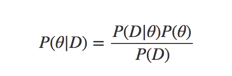
我們?yōu)榱饲蟮煤篁灧植迹枰ビ嬎鉖(D)
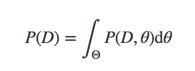
但是由于好多分布其參數(shù)空間非常大,很難計算P(D),于是就提出了數(shù)值逼近的方法,但是由于參數(shù)空間巨大,我們就要高效的去采樣,于是就有了mcmc方法,mcmc方法的一般套路:
- 先在參數(shù)空間中選擇一個
- 在參數(shù)空間中提議一個新的位置
- 根據(jù)先驗信息和觀測數(shù)據(jù)決定接收或者拒絕
- 如果接收跳躍,則跳轉(zhuǎn)到新的位置,并且返回到 step1
- 如果拒絕,則保持當前位置并返回到 step1
- 連續(xù)采用一系列點,最后返回接受的點集合
不同的 mcmc 算法的區(qū)別在于怎么選擇跳躍方式已經(jīng)如何決定是否跳躍,前面一篇貝葉斯統(tǒng)計:初學指南介紹了 Metropolis 對上述過程的處理,本文會介紹 Metropolis-Hastings 方法。
Metropolis-Hastings
先介紹算法的整個流程:

下面開始進行回答,為什么上面這個過程work?
首先我們需要上面的過程中,我們采樣出來是x是服從概率分布π(x)的,然后我們采樣的函數(shù)是一個k(x|x),那就有下面的公式:
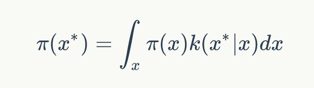
$$
\pi(x^) =
\int_{x}\pi(x)k(x^*|x)dx
$$
上面公式保證了如果我們按照k進行采樣,能夠保證新的采樣點和原先的點都是服從同一個分布的。
下面我們來證明如果細致平穩(wěn)條件成立:
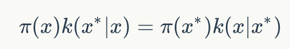
$$
\pi(x)k(x^|x) = \pi(x^)k(x|x^)
$$
則上面的積分也成立。
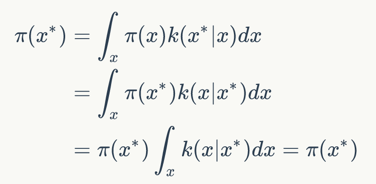
$$
\begin{align}
\pi(x^) & = \int_{x}\pi(x)k(x^|x)dx \
& = \int_{x} \pi(x^)k(x|x^)dx \
& = \pi(x^) \int_{x} k(x|x^)dx = \pi(x^)
\end{align}
$$
現(xiàn)在我們就證明了細致平穩(wěn)條件能保證x都服從同一分布。
下面我們繼續(xù)來看如何選擇k分布。
在 Metropolis-Hastings 中我們采取下面的策略:
- 從q(x|x)中采樣x
-
計算接收率
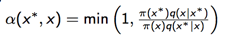
下面我們來證明上面的選取的k滿足細致平穩(wěn)條件:

下面我們來看下q(.)函數(shù)的選擇,q(.)函數(shù)的選擇一般有兩種:
- 對稱,如高斯分布,均勻分布,這種情況下稱為隨機游走
- 非對稱:如log-normal,傾向于選擇大的x值
下面是接收函數(shù),我們可以得到下面兩個點:
-
采樣值傾向于選擇高概率的點,因為

-
我們不希望采樣點來回震蕩,因為:
在上面一篇文章介紹的 Metropolis 算法中,q(.)函數(shù)就是對稱的,此時接收率就是:
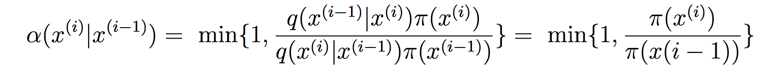
此時完全就是變?yōu)楹饬磕膫€參數(shù)更能描述數(shù)據(jù)了,更細致的說明可以看前面一篇文章貝葉斯統(tǒng)計:初學指南。
例子
假設我們有兩個時序數(shù)據(jù),xi,yi,其相關性為ρ,現(xiàn)在兩個之間的服從一個二元高斯分布:
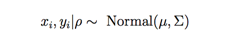

為簡單起見,我們假設σxx , σyy = 1。
此時我們可以寫出似然概率:
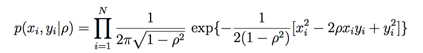
然后先驗概率如下:

最后我們可以得到后驗概率的近似:

下面我們就要通過mh方法來做的。
我們選擇q(.)為均勻分布:
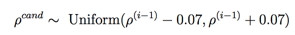
此時計算接受率則只計算p(ρ)即可,可以看代碼:
rho_candidate=uniform.rvs(rho-0.07,2*0.07)
accept=-3./2*log(1.-rho_candidate**2) - N*log((1.-rho_candidate**2)**(1./2)) - sum(1./(2.*(1.-rho_candidate**2))*(x**2-2.*rho_candidate*x*y+y**2))
計算的是log,方便計算,完整的代碼見mh
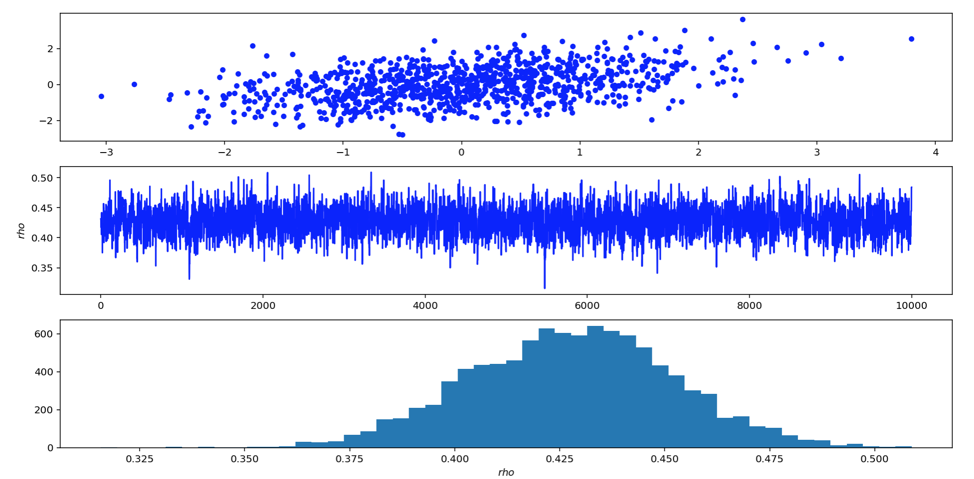
可以看到我們采樣后的ρ均值差不多就是0.4,符合我們的實際數(shù)據(jù)。
總結
文本介紹了MH算法,并且給出了為什么MH算法的證明,最后以一個簡單例子結尾,下面一篇我會繼續(xù)介紹Gibbs Sampling的,歡迎關注。
參考
Bayesian Inference: Metropolis-Hastings Sampling
你的鼓勵是我繼續(xù)寫下去的動力,期待我們共同進步。
