許多的語言都有好幾種不同的數字類型,比如C++,分別有int,float和double,外加各種變種long int, unsigned等等,實在是繁多,不過,JavaScript中,就只有一種數字類型——number。
比如,我們在瀏覽器的console中敲下下列代碼.
實際上,所有的數字類型,在JavaScript中,都是雙倍精度的浮點數類型,就和前面提到的C++的double一樣.按照標準,就是每一個數字,都是使用64位(8字節)來存儲.
要理解JavaScript中數字存儲特性,我們首先需要復習一下,在計算機中,是如何使用二進制來保存浮點數的.
浮點數的二進制表示
現今計算機浮點數的表示,都是采用了IEEE754標準,一個由Intel主導開發的標準,有興趣的同學可以了解一下上個世紀80年代的各種不同公司對于浮點數的表示,不過現在都已經按照標準來進行處理了.
任意一個浮點數都可以表示成如下的形式.
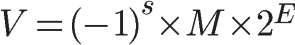
- 符號位(sign) (-1)^s表示的是符號位,當s=0時,V是正數,當s=1時,v為負數.
- 有效位(significand) M表示有效數字,范圍是[1,2)或者是[0,1)
-
指數(exponent) 2^E表示指數位.E的作用是對浮點數加權。
這種表示方式非常適合用于處理非常大或者非常接近0的數字.
了解的公式的表示,接下來,我們就可以對浮點數的位按照上述的三個變量進行劃分,分別對其進行編碼: - 1個單獨的符號位s用于編碼符號s.
- k位階碼字段,用以編碼指數E.
- n位冪字段,用以編碼尾數M.
下面,我們用C語言中的單精度浮點數(float)以及雙精度浮點數(double)進行說明.
單精度浮點數使用32bit來進行存儲,分別s=1, k=8以及n=23.其存儲結構如下圖所示

32位的存儲空間被分割成了三個部分,也就是對應上面所說的s,k以及n.
雙精度浮點數則是使用32位進行存儲,分別是s=1, k=11, n=52.
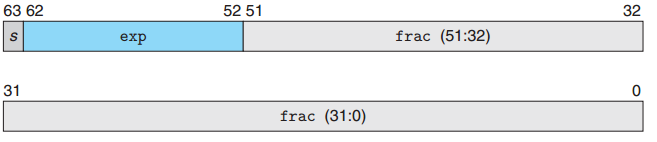
為了簡單起見,接下來使用單精度浮點數來進行說明.
單精度浮點數一共表示4種類型的數值,分別是:
-
規范化(Normalized)

-
非規范化(Denormalized)

-
無窮(Infinity)

- 非數字(NaN)

嚴格來說,Infinity以及NaN屬于同一類,因為他們的k相同,都是1,只是n上面的值不一樣,一個是全是0,另外一個全是1.
具體上就不展開講了,以后會另外開一篇新的文章來進行詳細講述計算機底層對于浮點數的存取.現在仍舊是Javascript的主場.我們要知道一點就是,根據浮點數的二進制表示形式,有一部分值是無法完全使用二進制準確表示的.就好比1/3這個值,在十進制上面,我們只能不斷的用0.3333333來無限循環表示,但是計算機表示一個浮點數的位是有限的,所以需要對多余的位進行截取,這一點就是誤差的來源.
知道了計算機中浮點數的二進制表示,我們都不難理解一些問題了,比如,JavaScript中的數字范圍是從-2^53到2^53.因此,JavaScript中的數字是非常適合用以做數學運算的,因為范圍非常的大,不容易導致溢出的問題.
位運算操作
許多的數學運算,都是以浮點數的形式直接計算的,比如:
0.1 * 1.9 // 0.19
-99 + 100 // 1
21 - 12.3 //8.7
但是,對于位運算則是比較特別,對于位運算,JavaScript會首先把浮點數轉換成32位的整型來進行處理,而不是直接對浮點型進行操作.準確的來說,是轉換成32位,大端序, 補碼的整型.(這里涉及到比較多操作系統的概念).
舉個例子
8 | 1 // 9
這個看起來很簡單的操作,8與1進行或運算,實際上經歷了好幾步的運算,才得到結果9,并不是一下子得出結果的.
正如前面所說,8和1一開始是64位的double,但是,他們在位運算的時候,會被轉換成32位的整型,對于數字8,則會轉換成00000000000000000000000000001000,我們可以驗證一下
(8).toString(2); // "1000"
同理,1則會轉換成00000000000000000000000000000001,把這兩個數分別按位進行或運算
00000000000000000000000000001000
00000000000000000000000000000001
--------------------------------
00000000000000000000000000001001
就會得到1001這一個數字,我們使用parseInt("1001", 2)對其進行轉換,結果就是9.
所有的位運算,都是按照上面所說的這一種方式來進行處理的.
- 把操作數轉換成32位整型
- 按位進行位運算
- 把得到的結果轉換會JavaScript浮點型屬性.
因為這些轉換都依賴于JavaScript的引擎,所以有部分引擎經過優化,就會把部分算術運算的操作數用整型來存儲,從而避免了一些無謂的轉換.
浮點數運算,可靠嗎?
說了這么多,什么64位雙精度浮點數,計算機儲存的方式等等,那么,JavaScript中的浮點數運算,可靠嗎?先來看一個例子:
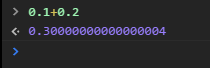
為什么上面得出的結果不是0.3,而是后面跟了一大堆0,后面還有個4?前面我們談到了浮點數的二進制存儲方式,我們知道,計算機僅僅可以使用二進制無限的接近部分浮點數,但是無法完全接近,即便64位浮點數以及可以很高精度的接近了,但是仍舊會產生誤差.浮點數的算術運算僅僅可以產生一個近似值,這個近似值接近于真實值.
有一個比較悲觀的事實就是,這些錯誤會隨著一系列的計算而累加起來,從而導致偏差越來越多,結果越來越不精確.
舉個例子,我們都知道
(x + y) + z = x + (y + z)
但是,這一點在計算機中,可不一定會成立.
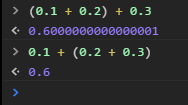
在部分計算機無法精確表達的浮點數產生的時候,就會導致誤差的產生.
這種誤差短期內還好,但是長期來說,是不可忍受的,假設是銀行或者金融機構使用node作為服務端進行處理,日積月累,就會發生許多的問題.
浮點數運算是不準確的,那么我們應該怎么避免這個問題呢?
一個很簡單的方法,就是避免浮點數的運算,把所有的運算都使用整型來進行.因為整型的運算是沒有省略近似的.例如,上面那個例子,我們換成這個
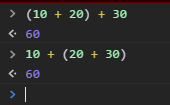
如果使用整型來進行算術運算,就不會產生上面的問題了,從而也保證了運算的精確性.
總結
- Javascript的數字類型是雙精度浮點型.
- 在Javascript中,整型是double的一個子集,而不是一個獨立的數據類型.
- Javascript在進行位運算的時候會把數字轉換成32位整型來進行處理.
- 浮點數運算是不準確的,擁有許多的局限性.