系列
目錄
1 Random Forest和Gradient Tree Boosting參數詳解
2 如何調參?
2.1 調參的目標:偏差和方差的協調
2.2 參數對整體模型性能的影響
2.3 一個樸實的方案:貪心的坐標下降法
2.3.1 Random Forest調參案例:Digit Recognizer
2.3.1.1 調整過程影響類參數
2.3.1.2 調整子模型影響類參數
2.3.2 Gradient Tree Boosting調參案例:Hackathon3.x
2.3.2.1 調整過程影響類參數
2.3.2.2 調整子模型影響類參數
2.3.2.3 殺一記回馬槍
2.4 “局部最優解”(溫馨提示:看到這里有彩蛋!)
2.5 類別不均衡的陷阱
3 總結
4 參考資料
1 Random Forest和Gradient Tree Boosting參數詳解
在sklearn.ensemble庫中,我們可以找到Random Forest分類和回歸的實現:RandomForestClassifier和RandomForestRegression,Gradient Tree Boosting分類和回歸的實現:GradientBoostingClassifier和GradientBoostingRegression。有了這些模型后,立馬上手操練起來?少俠請留步!且聽我說一說,使用這些模型時常遇到的問題:
明明模型調教得很好了,可是效果離我的想象總有些偏差?——模型訓練的第一步就是要定好目標,往錯誤的方向走太多也是后退。
憑直覺調了某個參數,可是居然沒有任何作用,有時甚至起到反作用?——定好目標后,接下來就是要確定哪些參數是影響目標的,其對目標是正影響還是負影響,影響的大小。
感覺訓練結束遙遙無期,sklearn只是個在小數據上的玩具?——雖然sklearn并不是基于分布式計算環境而設計的,但我們還是可以通過某些策略提高訓練的效率。
模型開始訓練了,但是訓練到哪一步了呢?——飽暖思淫欲啊,目標,性能和效率都得了滿足后,我們有時還需要有別的追求,例如訓練過程的輸出,袋外得分計算等等。
通過總結這些常見的問題,我們可以把模型的參數分為4類:目標類、性能類、效率類和附加類。下表詳細地展示了4個模型參數的意義:





# ★:默認值
不難發現,基于bagging的Random Forest模型和基于boosting的Gradient Tree Boosting模型有不少共同的參數,然而某些參數的默認值又相差甚遠。在《使用sklearn進行集成學習——理論》一文中,我們對bagging和boosting兩種集成學習技術有了初步的了解。Random Forest的子模型都擁有較低的偏差,整體模型的訓練過程旨在降低方差,故其需要較少的子模型(n_estimators默認值為10)且子模型不為弱模型(max_depth的默認值為None),同時,降低子模型間的相關度可以起到減少整體模型的方差的效果(max_features的默認值為auto)。另一方面,Gradient Tree Boosting的子模型都擁有較低的方差,整體模型的訓練過程旨在降低偏差,故其需要較多的子模型(n_estimators默認值為100)且子模型為弱模型(max_depth的默認值為3),但是降低子模型間的相關度不能顯著減少整體模型的方差(max_features的默認值為None)。
2 如何調參?
聰明的讀者應當要發問了:”博主,就算你列出來每個參數的意義,然并卵啊!我還是不知道無從下手啊!”
參數分類的目的在于縮小調參的范圍,首先我們要明確訓練的目標,把目標類的參數定下來。接下來,我們需要根據數據集的大小,考慮是否采用一些提高訓練效率的策略,否則一次訓練就三天三夜,法國人孩子都生出來了。然后,我們終于進入到了重中之重的環節:調整那些影響整體模型性能的參數。
2.1 調參的目標:偏差和方差的協調
同樣在《使用sklearn進行集成學習——理論》中,我們已討論過偏差和方差是怎樣影響著模型的性能——準確度。調參的目標就是為了達到整體模型的偏差和方差的大和諧!進一步,這些參數又可分為兩類:過程影響類及子模型影響類。在子模型不變的前提下,某些參數可以通過改變訓練的過程,從而影響模型的性能,諸如:“子模型數”(n_estimators)、“學習率”(learning_rate)等。另外,我們還可以通過改變子模型性能來影響整體模型的性能,諸如:“最大樹深度”(max_depth)、“分裂條件”(criterion)等。正由于bagging的訓練過程旨在降低方差,而boosting的訓練過程旨在降低偏差,過程影響類的參數能夠引起整體模型性能的大幅度變化。一般來說,在此前提下,我們繼續微調子模型影響類的參數,從而進一步提高模型的性能。
2.2 參數對整體模型性能的影響
假設模型是一個多元函數F,其輸出值為模型的準確度。我們可以固定其他參數,從而對某個參數對整體模型性能的影響進行分析:是正影響還是負影響,影響的單調性?
對Random Forest來說,增加“子模型數”(n_estimators)可以明顯降低整體模型的方差,且不會對子模型的偏差和方差有任何影響。模型的準確度會隨著“子模型數”的增加而提高。由于減少的是整體模型方差公式的第二項,故準確度的提高有一個上限。在不同的場景下,“分裂條件”(criterion)對模型的準確度的影響也不一樣,該參數需要在實際運用時靈活調整。調整“最大葉節點數”(max_leaf_nodes)以及“最大樹深度”(max_depth)之一,可以粗粒度地調整樹的結構:葉節點越多或者樹越深,意味著子模型的偏差越低,方差越高;同時,調整“分裂所需最小樣本數”(min_samples_split)、“葉節點最小樣本數”(min_samples_leaf)及“葉節點最小權重總值”(min_weight_fraction_leaf),可以更細粒度地調整樹的結構:分裂所需樣本數越少或者葉節點所需樣本越少,也意味著子模型越復雜。一般來說,我們總采用bootstrap對樣本進行子采樣來降低子模型之間的關聯度,從而降低整體模型的方差。適當地減少“分裂時考慮的最大特征數”(max_features),給子模型注入了另外的隨機性,同樣也達到了降低子模型之間關聯度的效果。但是一味地降低該參數也是不行的,因為分裂時可選特征變少,模型的偏差會越來越大。在下圖中,我們可以看到這些參數對Random Forest整體模型性能的影響:
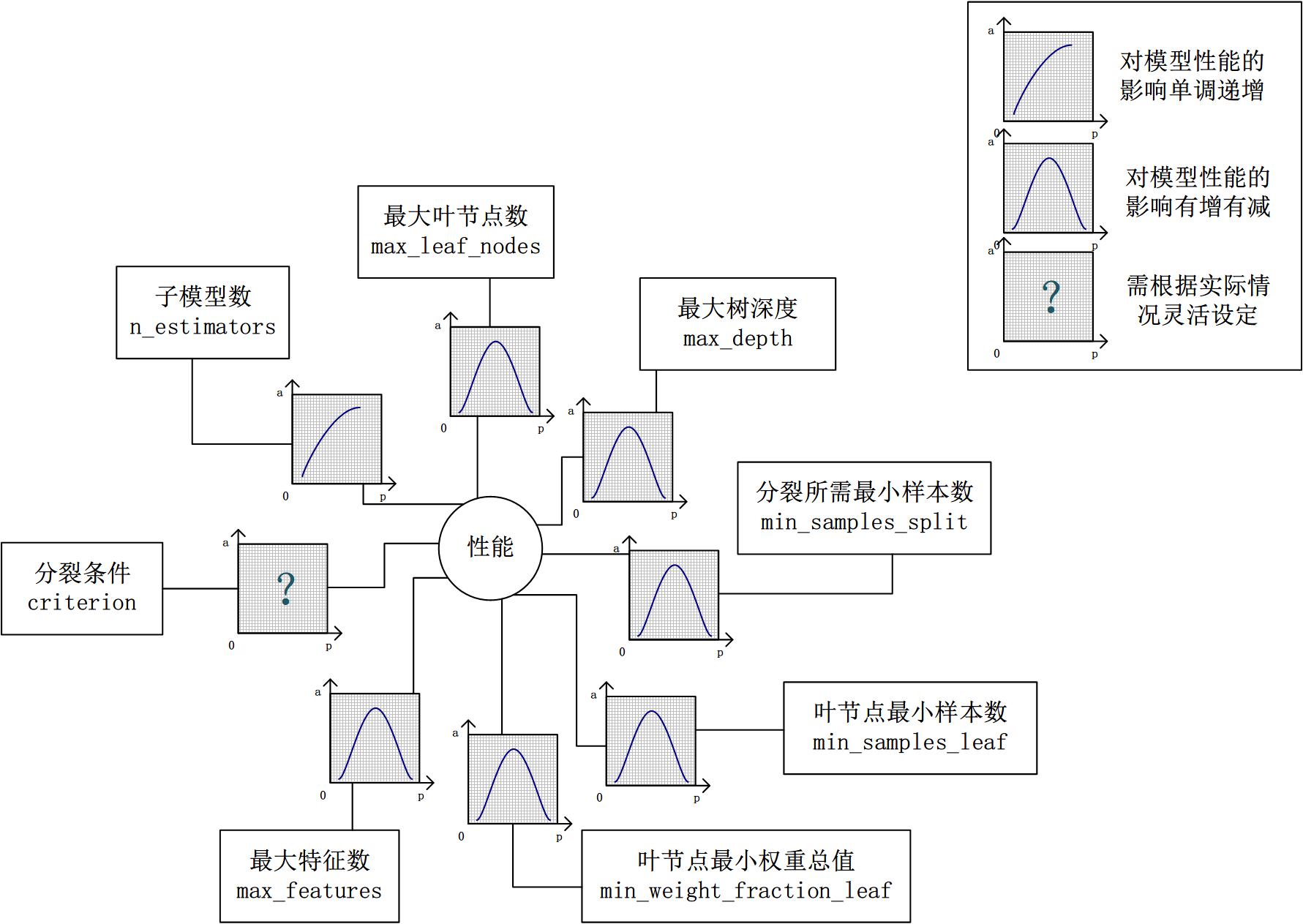
對Gradient Tree Boosting來說,“子模型數”(n_estimators)和“學習率”(learning_rate)需要聯合調整才能盡可能地提高模型的準確度:想象一下,A方案是走4步,每步走3米,B方案是走5步,每步走2米,哪個方案可以更接近10米遠的終點?同理,子模型越復雜,對應整體模型偏差低,方差高,故“最大葉節點數”(max_leaf_nodes)、“最大樹深度”(max_depth)等控制子模型結構的參數是與Random Forest一致的。類似“分裂時考慮的最大特征數”(max_features),降低“子采樣率”(subsample),也會造成子模型間的關聯度降低,整體模型的方差減小,但是當子采樣率低到一定程度時,子模型的偏差增大,將引起整體模型的準確度降低。還記得“初始模型”(init)是什么嗎?不同的損失函數有不一樣的初始模型定義,通常,初始模型是一個更加弱的模型(以“平均”情況來預測),雖說支持自定義,大多數情況下保持默認即可。在下圖中,我們可以看到這些參數對Gradient Tree Boosting整體模型性能的影響:

2.3 一個樸實的方案:貪心的坐標下降法
到此為止,我們終于知道需要調整哪些參數,對于單個參數,我們也知道怎么調整才能提升性能。然而,表示模型的函數F并不是一元函數,這些參數需要共同調整才能得到全局最優解。也就是說,把這些參數丟給調參算法(諸如Grid Search)咯?對于小數據集,我們還能這么任性,但是參數組合爆炸,在大數據集上,或許我的子子孫孫能夠看到訓練結果吧。實際上網格搜索也不一定能得到全局最優解,而另一些研究者從解優化問題的角度嘗試解決調參問題。
坐標下降法是一類優化算法,其最大的優勢在于不用計算待優化的目標函數的梯度。我們最容易想到一種特別樸實的類似于坐標下降法的方法,與坐標下降法不同的是,其不是循環使用各個參數進行調整,而是貪心地選取了對整體模型性能影響最大的參數。參數對整體模型性能的影響力是動態變化的,故每一輪坐標選取的過程中,這種方法在對每個坐標的下降方向進行一次直線搜索(line search)。首先,找到那些能夠提升整體模型性能的參數,其次確保提升是單調或近似單調的。這意味著,我們篩選出來的參數是對整體模型性能有正影響的,且這種影響不是偶然性的,要知道,訓練過程的隨機性也會導致整體模型性能的細微區別,而這種區別是不具有單調性的。最后,在這些篩選出來的參數中,選取影響最大的參數進行調整即可。
無法對整體模型性能進行量化,也就談不上去比較參數影響整體模型性能的程度。是的,我們還沒有一個準確的方法來量化整體模型性能,只能通過交叉驗證來近似計算整體模型性能。然而交叉驗證也存在隨機性,假設我們以驗證集上的平均準確度作為整體模型的準確度,我們還得關心在各個驗證集上準確度的變異系數,如果變異系數過大,則平均值作為整體模型的準確度也是不合適的。在接下來的案例分析中,我們所談及的整體模型性能均是指平均準確度,請各位留心。
2.3.1 Random Forest調參案例:Digit Recognizer
在這里,我們選取Kaggle上101教學賽中的Digit Recognizer作為案例來演示對RandomForestClassifier調參的過程。當然,我們也不要傻乎乎地手工去設定不同的參數,然后訓練模型。借助sklearn.grid_search庫中的GridSearchCV類,不僅可以自動化調參,同時還可以對每一種參數組合進行交叉驗證計算平均準確度。
2.3.1.1 調整過程影響類參數
首先,我們需要對過程影響類參數進行調整,而Random Forest的過程影響類參數只有“子模型數”(n_estimators)。“子模型數”的默認值為10,在此基礎上,我們以10為單位,考察取值范圍在1至201的調參情況:
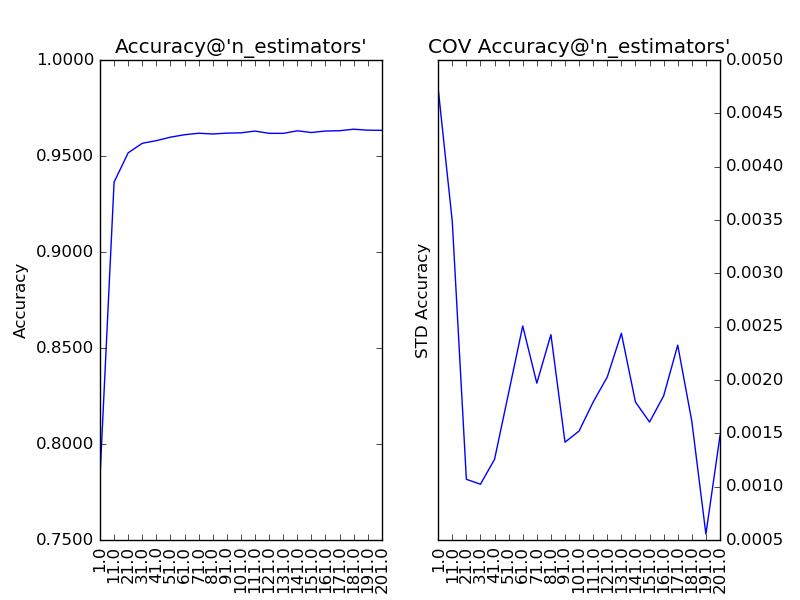
通過上圖我們可以看到,隨著“子模型數”的增加,整體模型的方差減少,其防止過擬合的能力增強,故整體模型的準確度提高。當“子模型數”增加到40以上時,準確度的提升逐漸不明顯。考慮到訓練的效率,最終我們選擇“子模型數”為200。此時,在Kaggle上提交結果,得分為:0.96500,很湊合。
2.3.1.2 調整子模型影響類參數
在設定“子模型數”(n_estimators)為200的前提下,我們依次對子模型影響類的參數對整體模型性能的影響力進行分析。
對“分裂條件”(criterion)分別取值gini和entropy,得到調參結果如下:
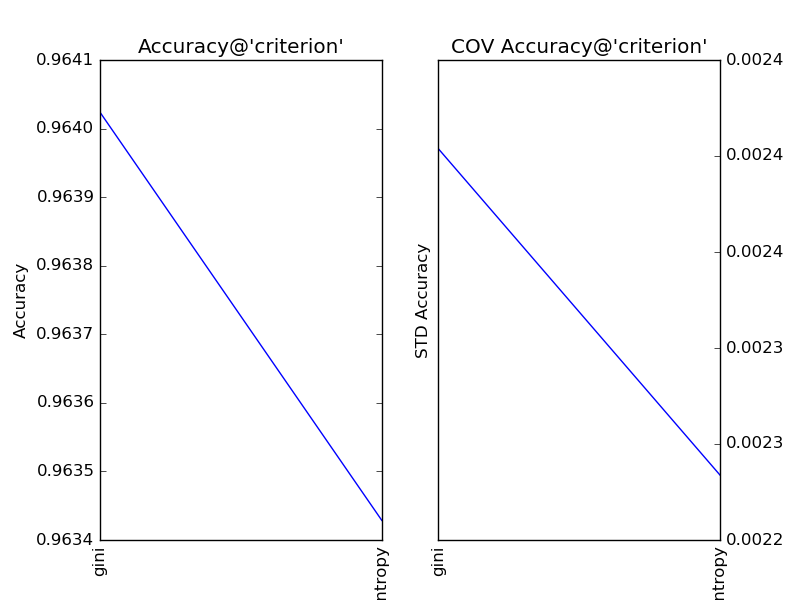
顯見,在此問題中,“分裂條件”保持默認值gini更加合適。
對“分裂時參與判斷的最大特征數”(max_feature)以1為單位,設定取值范圍為28至47,得到調參結果如下:
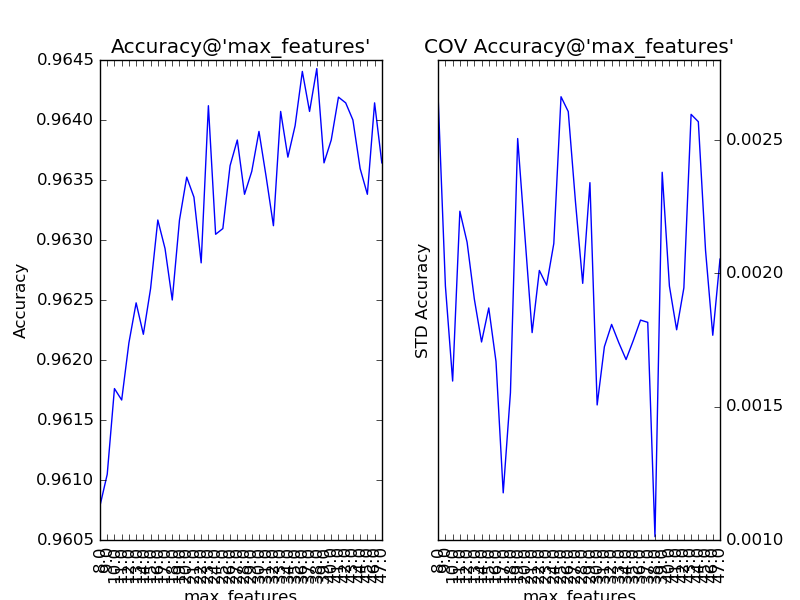
“分裂時參與判斷的最大特征數”的默認值auto,即總特征數(sqrt(784)=28)的開方。通過提升該參數,整體模型的準確度得到了提升。可見,該參數的默認值過小,導致了子模型的偏差過大,從而整體模型的偏差過大。同時,我們還注意到,該參數對整體模型性能的影響是近似單調的:從28到38,模型的準確度逐步抖動提升。所以,我們可考慮將該參數納入下一步的調參工作。
對“最大深度”(max_depth)以10為單位,設定取值范圍為10到100,得到調參結果如下:

隨著樹的深度加深,子模型的偏差減少,整體模型的準確度得到提升。從理論上來說,子模型訓練的后期,隨著方差增大,子模型的準確度稍微降低,從而影響整體模型的準確度降低。看圖中,似乎取值范圍從40到60的情況可以印證這一觀點。不妨以1為單位,設定取值范圍為40到59,更加細致地分析:
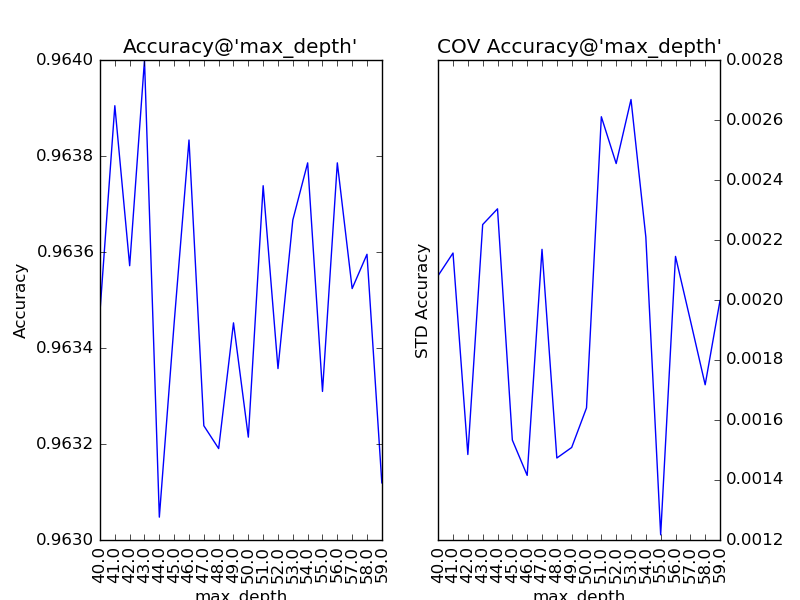
有點傻眼了,怎么跟預想的不太一樣?為什么模型準確度的變化在40到59之間沒有鮮明的“規律”了?要分析這個問題,我們得先思考一下,少一層子節點對子模型意味著什么?若少的那一層給原子模型帶來的是方差增大,則新子模型會準確度提高;若少的那一層給原子模型帶來的是偏差減小,則新子模型會準確度降低。所以,細粒度的層次變化既可能使整體模型的準確度提升,也可能使整體模型的準確度降低。從而也說明了,該參數更適合進行粗粒度的調整。在訓練的現階段,“抖動”現象的發生說明,此時對該參數的調整已不太合適了。
對“分裂所需的最小樣本數”(min_samples_split)以1為單位,設定取值范圍為2到11,得到調參的結果:
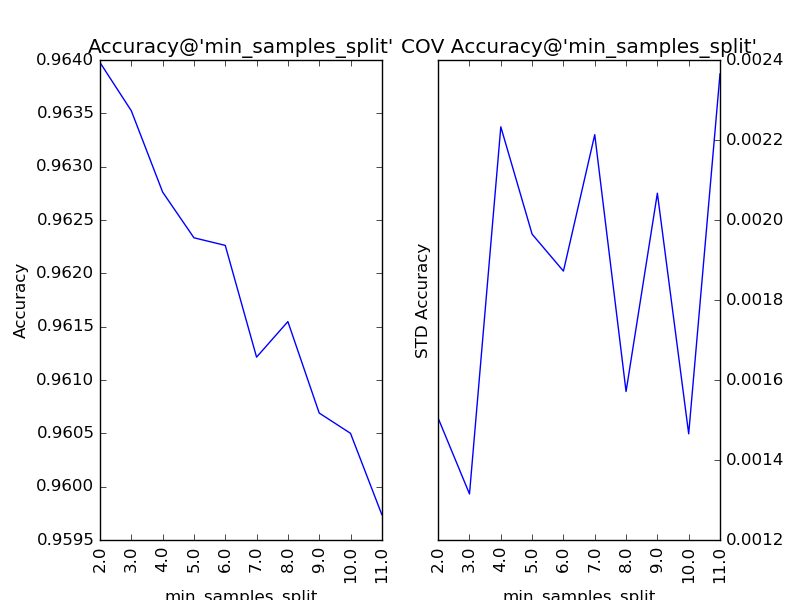
我們看到,隨著分裂所需的最小樣本數的增加,子模型的結構變得越來越簡單,理論上來說,首先應當因方差減小導致整體模型的準確度提升。但是,在訓練的現階段,子模型的偏差增大的幅度比方差減小的幅度更大,所以整體模型的準確度持續下降。該參數的默認值為2,調參后,最優解保持2不變。
對“葉節點最小樣本數”(min_samples_leaf)以1為單位,設定取值范圍為1到10,得到調參結果如下:
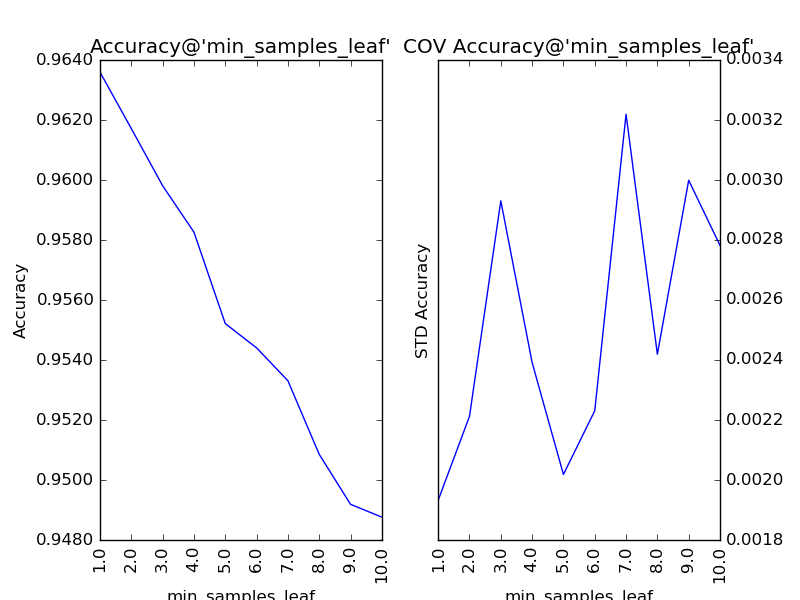
同“分裂所需的最小樣本數”,該參數也在調參后,保持最優解1不變。
對“最大葉節點數”(max_leaf_nodes)以100為單位,設定取值范圍為2500到3400,得到調參結果如下:
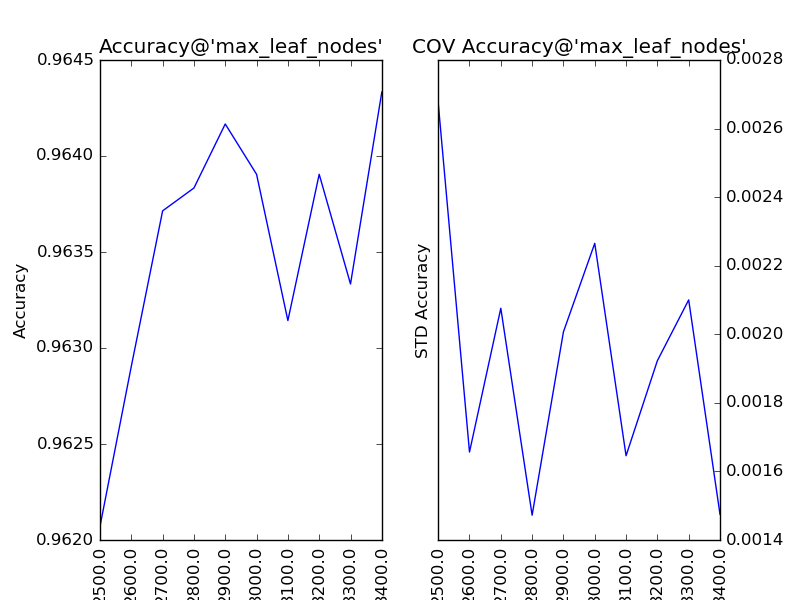
類似于“最大深度”,該參數的增大會帶來模型準確的提升,可是由于后期“不規律”的抖動,我們暫時不進行處理。
通過對以上參數的調參情況,我們可以總結如下:

接下來,我們固定分裂時參與判斷的最大特征(max_features)為38,在Kaggle上提交一次結果:0.96671,比上一次調參好了0.00171,基本與我們預期的提升效果一致。
還需要繼續下一輪坐標下降式調參嗎?一般來說沒有太大的必要,在本輪中出現了兩個發生抖動現象的參數,而其他參數的調整均沒有提升整體模型的性能。還是得老調重彈:數據和特征決定了機器學習的上限,而模型和算法只是逼近這個上限而已。在DR競賽中,與其期待通過對RandomForestClassifier調參來進一步提升整體模型的性能,不如挖掘出更有價值的特征,或者使用自帶特征挖掘技能的模型(正如此題,圖分類的問題更適合用神經網絡來學習)。但是,在這里,我們還是可以自信地說,通過貪心的坐標下降法,比那些用網格搜索法窮舉所有參數組合,自以為得到最優解的朋友們更進了一步。
2.3.2 Gradient Tree Boosting調參案例:Hackathon3.x
在這里,我們選取Analytics Vidhya上的Hackathon3.x作為案例來演示對GradientBoostingClassifier調參的過程。
2.3.2.1 調整過程影響類參數
GradientBoostingClassifier的過程影響類參數有“子模型數”(n_estimators)和“學習率”(learning_rate),我們可以使用GridSearchCV找到關于這兩個參數的最優解。慢著!這里留了一個很大的陷阱:“子模型數”和“學習率”帶來的性能提升是不均衡的,在前期會比較高,在后期會比較低,如果一開始我們將這兩個參數調成最優,這樣很容易陷入一個“局部最優解”。在目標函數都不確定的情況下(如是否凸?),談局部最優解就是耍流氓,本文中“局部最優解”指的是調整各參數都無明顯性能提升的一種狀態,所以打了引號。下圖中展示了這個兩個參數的調參結果:
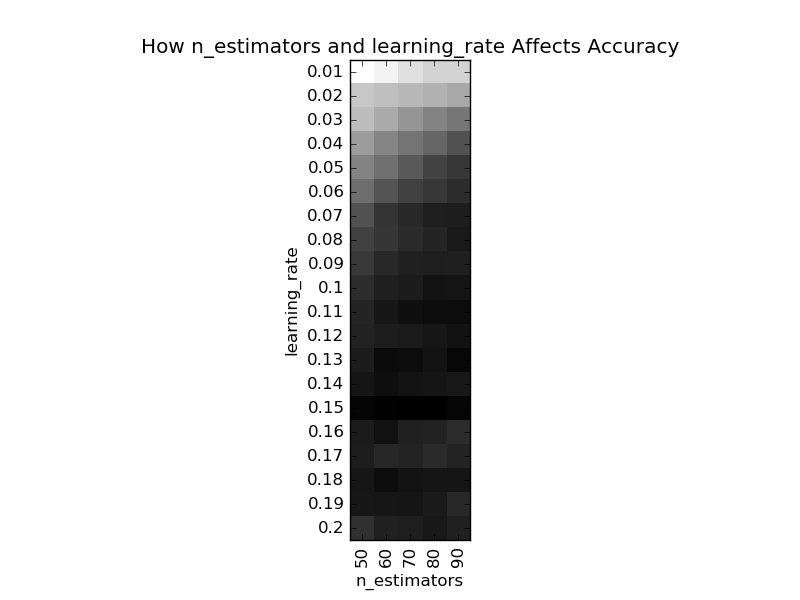
在此,我們先直覺地選擇“子模型數”為60,“學習率”為0.1,此時的整體模型性能(平均準確度為0.8253)不是最好,但是也不差,良好水準。
2.3.2.2 調整子模型影響類參數
對子模型影響類參數的調整與Random Forest類似。最終我們對參數的調整如下:

到此,整體模型性能為0.8313,與workbench(0.8253)相比,提升了約0.006。
2.3.2.3 殺一記回馬槍
還記得一開始我們對“子模型數”(n_estimators)和“學習率”(learning_rate)手下留情了嗎?現在我們可以回過頭來,調整這兩個參數,調整的方法為成倍地放大“子模型數”,對應成倍地縮小“學習率”(learning_rate)。通過該方法,本例中整體模型性能又提升了約0.002。
2.4 “局部最優解”
目前來說,在調參工作中,廣泛使用的仍是一些經驗法則。Aarshay Jain對Gradient Tree Boosting總結了一套調參方法,其核心思想在于:對過程影響類參數進行調整,畢竟它們對整體模型性能的影響最大,然后依據經驗,在其他參數中選擇對整體模型性能影響最大的參數,進行下一步調參。這種方法的關鍵是依照對整體模型性能的影響力給參數排序,然后按照該順序對的參數進行調整。如何衡量參數對整體模型性能的影響力呢?基于經驗,Aarshay提出他的見解:“最大葉節點數”(max_leaf_nodes)和“最大樹深度”(max_depth)對整體模型性能的影響大于“分裂所需最小樣本數”(min_samples_split)、“葉節點最小樣數”(min_samples_leaf)及“葉節點最小權重總值”(min_weight_fraction_leaf),而“分裂時考慮的最大特征數”(max_features)的影響力最小。
Aarshay提出的方法和貪心的坐標下降法最大的區別在于前者在調參之前就依照對整體模型性能的影響力給參數排序,而后者是一種“很自然”的貪心過程。還記得2.3.2.1小節中我們討論過“子模型數”(n_estimators)和“學習率”(learning_rate)的調參問題嗎?同理,貪心的坐標下降法容易陷入“局部最優解”。對Random Forest調參時會稍微好一點,因為當“子模型數”調到最佳狀態時,有時就只剩下諸如““分裂時參與判斷的最大特征數”等Aarshay認為影響力最小的參數可調了。但是,對Gradient Tree Boosting調參時,遇到“局部最優解”的可能性就大得多。
Aarshay同樣對Hackathon3.x進行了調參試驗,由于特征提取方式的差異,參數賦值相同的情況下,本文的整體模型性能仍與其相差0.007左右(唉,不得不再說一次,特征工程真的很重要)。首先,在過程影響類參數的選擇上,Aarshay的方法與貪心的坐標下降法均選擇了“子模型數”為60,“學習率”為0.1。接下來,Aarshay按照其定義的參數對整體模型性能的影響力,按序依次對參數進行調整。當子模型影響類參數確定完成后,Aarshay的方法提升了約0.008的整體模型性能,略勝于貪心的坐標下降法的0.006。但是,回過頭來繼續調試“子模型數”和“學習率”之后,Aarshay的方法又提升了約0.01的整體模型性能,遠勝于貪心的坐標下降法的0.002。
誒!誒!誒!少俠請住手!你說我為什么要在這篇博文中介紹這種“無用”的貪心的坐標下降法?首先,這種方法很容易憑直覺就想到。人們往往花了很多的時間去搞懂模型的參數是什么含義,對整體模型性能有什么影響,搞懂這些已經不易了,所以接下來很多人選擇了最直觀的貪心的坐標下降法。通過一個實例,我們更容易記住這種方法的局限性。除了作為反面教材,貪心的坐標下降法就沒有意義了嗎?不難看到,Aarshay的方法仍有改進的地方,在依次對參數進行調整時,還是需要像貪心的坐標下降法中一樣對參數的“動態”影響力進行分析一下,如果這種影響力是“抖動”的,可有可無的,那么我們就不需要對該參數進行調整。
2.5 類別不均衡的陷阱
哈哈哈,這篇博文再次留了個陷阱,此段文字并不是跟全文一起發布!有人要說了,按照我的描述,Aarshay的調參試驗不可再現啊!其實,我故意沒說Aarshay的另一個關鍵處理:調參前的參數初始值。因為Hackathon3.x是一個類別不均衡的問題,所以如果直接先調試“最大深度”(max_depth),會發現其會保持默認值3作為最優解,而后面的調參中,“分裂所需最小樣本數”(min_samples_split)、“葉節點最小樣本數”(min_samples_leaf)再怎么調都沒有很大作用。這是因為,正例樣本遠遠小于反例,所以在低深度時,子模型就可能已經對正例過擬合了。所以,在類別不均衡時,只有先確定“葉節點最小樣本數”(min_samples_leaf),再確定“分裂所需最小樣本數”(min_samples_split),才能確定“最大深度”。而Aarshay設定的初始值,則以經驗和直覺避開了這個險惡的陷阱。
如果實在覺得經驗和直覺不靠譜,我還嘗試了一種策略:首先,我們需要初步地調一次“子采樣率”(subsample)和“分裂時考慮的最大特征數”(max_features),在此基礎上依次調好“葉節點最小樣本數”(min_samples_leaf)、“分裂所需最小樣本數”(min_samples_split)以及“最大深度”(max_depth)。然后,按照Aarshay的方法,按影響力從大到小再調一次。通過這種方法,整體模型性能在未等比縮放過程影響類參數前,已達到約0.8352左右,比workbench相比,提升了約0.1,與Aarshay的調參試驗差不多,甚至更好一點點。
回過頭來,我們再次看看貪心的坐標下降法是怎么掉入這個陷阱的。在確定過程影響類參數后,貪心的坐標下降法按照“動態”的對整體模型性能的影響力大小,選擇了“葉節點最小樣本數”進行調參。這一步看似和上一段的描述是一致的,但是,一般來說,含隨機性(“子采樣率”和“分裂時考慮的最大特征數”先初步調過)的“葉節點最小樣本數”要大于無隨機性。舉個例來說,因為增加了隨機性,導致了子采樣后,某子樣本中只有一個正例,且其可以通過唯一的特征將其分類,但是這個特征并不是所有正例的共性,所以此時就要求“葉節點最小樣本數”需要比無隨機性時大。對貪心的坐標下降來說,“子采樣率”和“分裂時考慮的最大特征數”在當下,對整體模型性能的影響比不上“葉節點最小樣本數”,所以栽了個大跟頭。
3 總結
在這篇博文中,我一反常態,花了大部分時間去試驗和說明一個有瑕疵的方案。數據挖掘的工作中的方法和技巧,有很大一部分暫時還未被嚴謹地證明,所以有很大部分人,特別是剛入門的小青年們(也包括曾經的我),誤以為其是一門玄學。實際上,盡管沒有被嚴謹地證明,我們還是可以通過試驗、分析,特別是與現有方法進行對比,得到一個近似的合理性論證。
另外,小伙伴們你們有什么獨到的調參方法嗎?請不要有絲毫吝嗇,狠狠地將你們的獨門絕技全釋放在我身上吧,請大膽留言,殘酷批評!
4 參考資料
1、《使用sklearn進行集成學習——理論》
2、Complete Guide to Parameter Tuning in Gradient Boosting (GBM) in Python