一些聚類算法
Birch層次聚類 ,KMeans原形算法 ,AGNES層次算法, DBSCAN密度算法, LVQ原形算法
簡單做一個個人想法記錄,其實聚類算法來說大體上的思路都非常簡單,無非是找點或者區域,計算它們之間的距離(這個距離為抽象意義上的距離,不同的內容有不同的距離表示方式),然后根據一定規則(一般都是以最近為相鄰),然后疊加在一起。
簡單來說:聚類就是如何確認某些點或區域,再根據這些選好的點與區域再進行距離計算,從而進行劃分。
簡單代碼可見:https://github.com/AresAnt/ML-DL
Kmeans算法:(原形聚類方法)
最簡單的Kmeans算法的思路,首先我們要確定劃分幾個類(即K值)。
假設這里需要劃分3個類:
- 先初始化三個隨機樣本點。(隨機點一定是要在樣本范圍之內,一般來說可以以隨機挑選三個樣本點作為起始樣本點)
- 對全樣本進行遍歷,與三個隨機點進行計算,與哪個隨機點近就劃分進入哪個隨機點的區域內。
- 一次劃分完畢后,對區域內所有的點間距離進行平均計算。假設當前區域內劃分進來了m-1個樣本點,加上隨機點,總共為m個樣本在這片區域內。兩兩計算它們之間的距離,總共需要循環計算 m (m-1) 次,然后除以這片區域內的樣本數量。即
$$ {\frac{1}{m}}{\sum^{m}_{i=1,i<j}λ_iλ_j}$$ - 算出后的點,即為新的隨機樣本點(也稱為算質心),然后重復以上的過程,不斷的更替質心直到最后確定。
LVQ算法:(原形聚類方法)
LVQ算法是假設數據樣本帶有類別標記的,學習過程中利用樣本的這些監督信息來輔助聚類。
(簡單描述,其實它的做法與KMeans類似,也是相當于是一個找質心點的過程,這里為找原形向量,每一行的向量其實對應的就是上述所提到的質心點)
算法流程:
輸入:樣本集D = {(x1,y1),(x2,y2),....,(xm,ym)} (設 D1 = (x1,y1))
原形向量的個數q,各原形向量的類別標記 { t1,t2,t3,t4,..,tq } 【這個劃分的意思是指,假設我上述樣本集中的 yi 為兩類,即 0,1, 那么我可以設置原形向量的類別為 { 1,1,0,0,1} (意思為1分類的樣本最后會劃分為3個簇,0分類的樣本最后會劃分為2個簇】
學習率 α (0~1)
過程:
- 初始化一組原形向量 P = {(p1,t1),(p2,t2) ,...,(pq,tq)} (這個初始化一般以隨機改 ti
分類下的樣本作為 pi)
# 初始化原形向量,這里做簡單操作,假設希望找到 3個好瓜的簇,2個壞瓜的簇,總共五個簇
good = np.where(rowdata_y == 1)[0]
bad = np.where(rowdata_y == 0)[0]
vectorlist = random.sample(list(good),3) + random.sample(list(bad),2)
P_x = np.zeros((k,rowdata_x.shape[1]))
P_y = np.zeros((k,rowdata_y.shape[1]))
for i in range(len(vectorlist)):
P_x[i] = rowdata_x[vectorlist[i]]
P_y[i] = rowdata_y[vectorlist[i]]
- 循環迭代:
從樣本 D 中隨機抽取一個樣本(xi,yi)進行向量校正(類似前面的移動質心點)
找出最小的原形向量 pj
if D.yi == P.tj:
P.pj = P.pj + α * ( D.xi - P.pj )
else:
P.pj = P.pj - α * ( D.xi - P.pj )
- 輸出原形向量 P
缺點:LVQ算法的質心點移動取決于進來計算的隨機點,這個點的進來順序有關,如果進來的點都過于的奇特,那么質心點的改變也會特別的奇怪。需要一定量的迭代次數來進行更正。不過因為隨機點是隨機產生,隨機產生符合正太分布,正態分布的點數為樣本中心點質量有關。
AGNES 層次聚類算法:(層次聚類算法)
層次聚類算法可以有“自底向上”的聚合策略,也可以采用“自頂向下”的分拆策略。(2分-Kmeans就是“自頂向下”的策略)
AGNES是“自底向上”的聚合策略,它簡單的先將每個樣本點看做是一個簇,然后通過計算相應的距離,選取最小的兩個簇合成為以個簇,以此反復,計算量龐大。
算法思路,對于數據集D,D={x_1,x_2,…,x_n}:
將數據集中的每個對象生成一個簇,得到簇列表C,C={c_1,c_2,…,c_n}
a) 每個簇只包含一個數據對象:c_i={x_i};
重復如下步驟,直到C中只有一個簇:
a) 從C中的簇中找到兩個“距離”最近的兩個簇:min?〖D(c_i,c_j)〗;
b) 合并簇c_i和cj,形成新的簇c(i+j);
c) 從C中刪除簇c_i和cj,添加簇c(i+j)
稍微注意一下簇間距離運算的方式:
在上面描述的算法中涉及到計算兩個簇之間的距離,對于簇C_1和C_2,計算〖D(C_1,C〗_2),有以下幾種計算方式:
單連鎖(Single link):
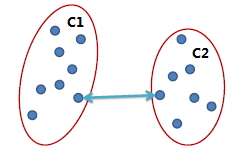
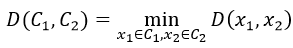
兩個簇之間最近的兩個點的距離作為簇之間的距離,該方式的缺陷是受噪點影響大,容易產生長條狀的簇。
全連鎖(Complete link)
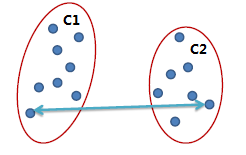

兩個簇之間最遠的兩個點的距離作為簇之間的距離,采用該距離計算方式得到的聚類比較緊湊。
平均連鎖(Average link)


兩個簇之間兩兩點之間距離的平均值,該方式可以有效地排除噪點的影響。
Birch層次聚類算法:(層次聚類算法)
不做多余贅述,可以查看該鏈接:http://www.lxweimin.com/p/e0c4f19f7ab1
DBSCAN密度聚類算法:(密度聚類算法)
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪聲的基于密度的聚類方法)是一種基于密度的空間聚類算法。該算法將具有足夠密度的區域劃分為簇,并在具有噪聲的空間數據庫中發現任意形狀的簇,它將簇定義為密度相連的點的最大集合。
該算法利用基于密度的聚類的概念,即要求聚類空間中的一定區域內所包含對象(點或其他空間對象)的數目不小于某一給定閾值。DBSCAN算法的顯著優點是聚類速度快且能夠有效處理噪聲點和發現任意形狀的空間聚類。但是由于它直接對整個數據庫進行操作且進行聚類時使用了一個全局性的表征密度的參數,因此也具有兩個比較明顯的弱點:
(1)當數據量增大時,要求較大的內存支持I/O消耗也很大;
(2)當空間聚類的密度不均勻、聚類間距差相差很大時,聚類質量較差
DBSCAN密度聚類算法從樣本的密度角度來考察樣本之間的可連接性。簡單來說,就是對一個樣本點它,以它為中心,它周邊一定區域內所含樣本數達到閾值,則該樣本點就屬于一個領域內,且該樣本所含區域范圍內的樣本點即為一個密度云,然后進行向外擴充。
基本定義:
- 領域:對于 xj 屬于 數據集D,其領域包含樣本集與xj的距離不大于 γ 的樣本,即 N(xj) = { xj屬于D | dist ( xi , xj ) <= γ }
- 核心對象: 若 xj 的領域中至少包含 MinPts 個樣本,即 | N(xj)| >= MinPts ,則 xj 為一個核心對象
- 密度直達: 若xj位于xi的領域中,且xi也是一個核心對象,則稱xj有xi密度直達
- 密度可達: 對xi與xj,若存在樣本序列 p1,p2,..,pn,其中 p1 = xi , pn = xj ,且 pi+1 是由 pi 密度直達,則稱xj由xi密度可達
- 密度相連:對xi與xj,若存在xk使得xi,xj均有xk密度可達,則xi,xj密度相連【我們做聚類主要就是找到一個樣本點(簡稱密度云)的最大密度相連】
算法流程:
輸入:樣本集 D = { x1,x2,x3,...,xn }
領域參數 { γ , MinPts}
過程:
- 先找出整個樣本中的核心對象集合 T
- 隨機選取核心對象集合中的一個對象作為起始對象,尋找它的領域樣本點集 L
- 對尋找出來的樣本點集 L 做核心對象判斷,符合核心對象的形成一個新的小核心對象點集 P,再對 P 重復第二步,直到循環結束輸出一個全體的樣本點集 E
- 原來的核心對象集合 T - E ,留下來的為剩下的核心對象集合, E 為分好的簇,重復第二步直到核心對象集合 T 中沒有核心對象
高斯混合聚類(概率模型聚類)
簡單來說這個聚類方式就是,我事先告訴算法有需要有幾個分類,然后通過隨機樣本,然后以隨機后的樣本求其后驗分布。求出其后驗分布后(簇的劃分即為后驗概率最大的一方)。再通過求出的后驗概率去對原先假設的樣本進行更新迭代,使其趨向于最優解(這時候就是通過極大似然估計去逼近最優值,來更新樣本)這里我們可以假設我們的分類概率是一個隱變量,那么這樣子的求解方式就是EM算法:詳見(另一篇文章)
其實EM算法與反向傳播的概念基本上是相同,在反向傳播中,我們先假設一個參數求出一個 y值解,將這個解值去與真實值比較,后會產生一個損失函數,目的是使損失函數不斷的減小從而更新假設值。EM算法其實也是相同的,稍微不同的是,這里沒有真實值去進行逼近,而是通過對每次的假設與極大似然估計進行逼近,在兩者達到一定閾值或者到一定迭代次數時候即為最佳。
算法流程:
輸入:樣本集 D = { x1,x2,x3,...,xm }
高斯混合成分個數k
過程:
初始化高斯混合分布函數 a,u,Z
a = 1 / k
u = 隨機的選擇連續函數在高斯分布中的值
Z = (還有待研究)
- 先計算其所有的樣本K的對于D中每個樣本的后驗概率
- 更新a,u,Z的值(通過極大似然估計),迭代循環到第一步
- 根據后驗概率選擇分類