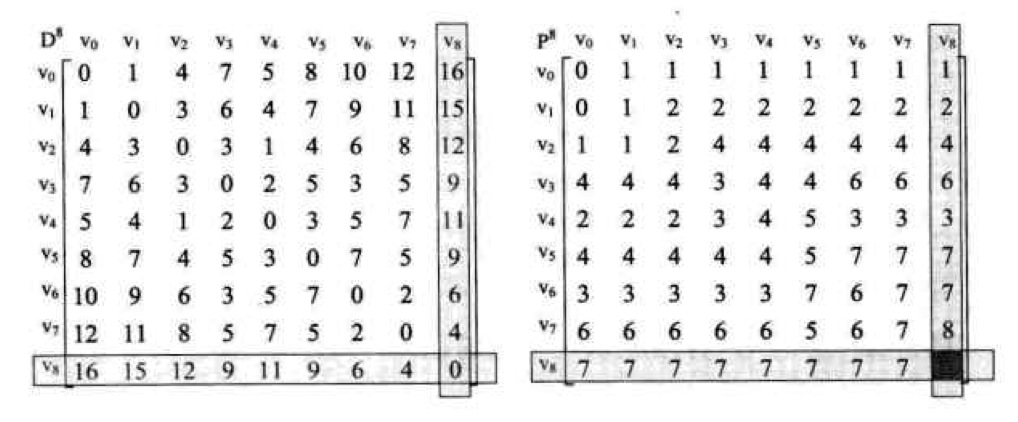
圖_最短路徑(個人認為應該叫最佳路徑)
最短路徑其實說的是權重,請仔細理解權重的意義。在實際應用中,權重可以是消耗的時間、金錢、距離甚至是概率等等,我們求最短路徑,也就是求這些權重之和的最小(或最大)值
北京地鐵復雜的線路圖,從育新小區到公益西橋有很多條線路可以選擇,從時間、距離、還有車費等不同的角度考慮,可能獲得的最佳線路都不一樣~~~
迪杰斯特拉(Dijkstra)算法
(兩個頂點之間的最短路徑)
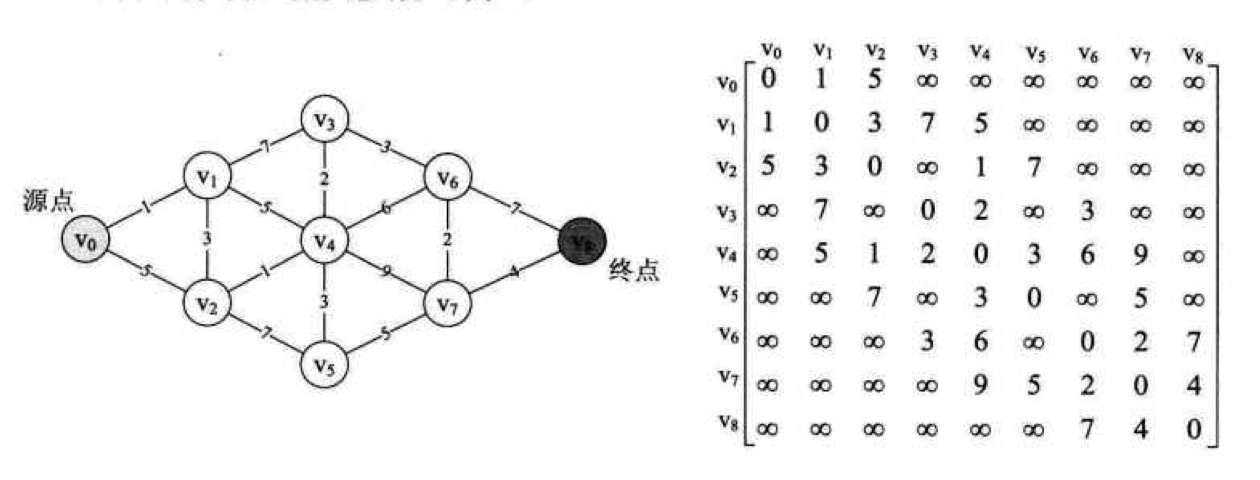
按照路徑長度遞增的產生最短路徑的算法,也就是說不是一次性算出兩個定點之間的最短距離,而是通過計算每個中間頂點的最短距離,最后推導出要求的頂點最短距離


- 5~12行是初始化階段,final一維數組值均為0,D數組記錄所有頂點到v0的最短路徑值,當前是{65535,1,5,65535,65535,65535,65535,65535,65535},p數組全為0,表示目前還沒有找到任意一個頂點的最短路徑
- 13行是一個主循環,每循環一次求得v0與一個頂點的最短路徑,也就是讓一個頂點的final值為1
- 16~24行的循環,先令min為65535,通過w循環,與D[w]比較,找到目前最小的min和k值。當前是:D[1]的值最小,因為在第一次初始化的時候,v0連接的就兩條邊,v1和v2,如果是第二次循環,那就是D[2]
- 25~32行,是在修正之前已經判定的v0和某個點的最短距離,例如:在初始化的時候v0到v2的最短距離是5,但是第一次循環完成之后,發現v0->v1=min=1,v1->v2=3,因此v0->v1->v2=min+G.matirx[v1][v2]=4,這個值是小于D[2]=5的
佛洛伊德(floyd)算法
能計算出北京地鐵所有站與站之間在時間上的最佳路徑,那所有上班族就知道該怎么換乘才最省時間!!!
(所有頂點到其他頂點之間的最短距離)
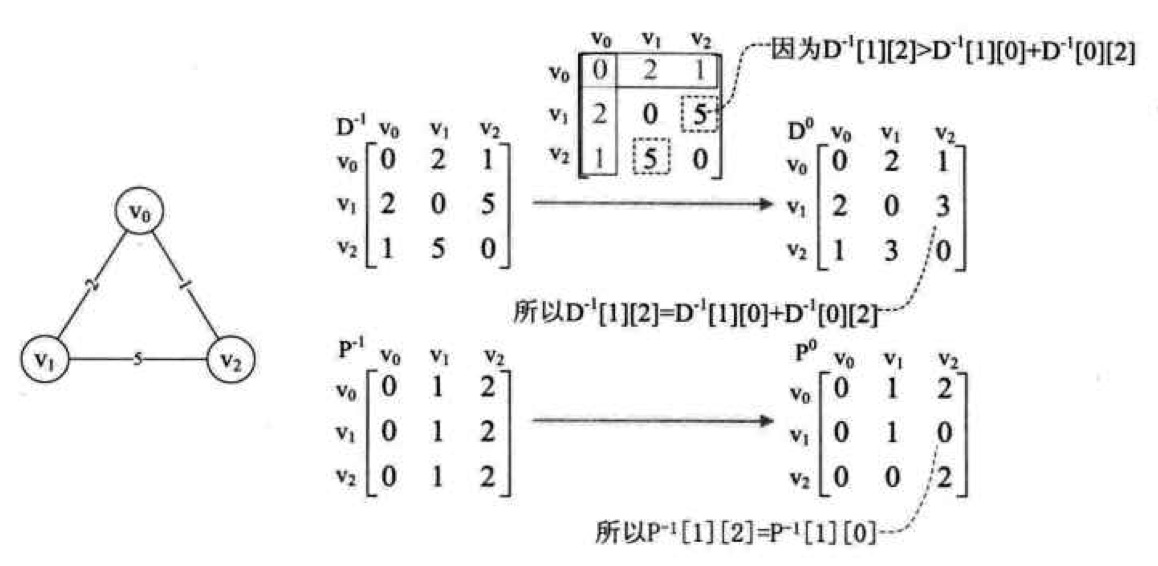
上面這個公式的含義就是:我們要判斷所有頂點經過k頂點到達另一個頂點的最短路徑。例如:v->w > v->k->w,整個算法就是根據這個簡單的邏輯推導出所有頂點到其他頂點的最短路徑,看看下面的圖:
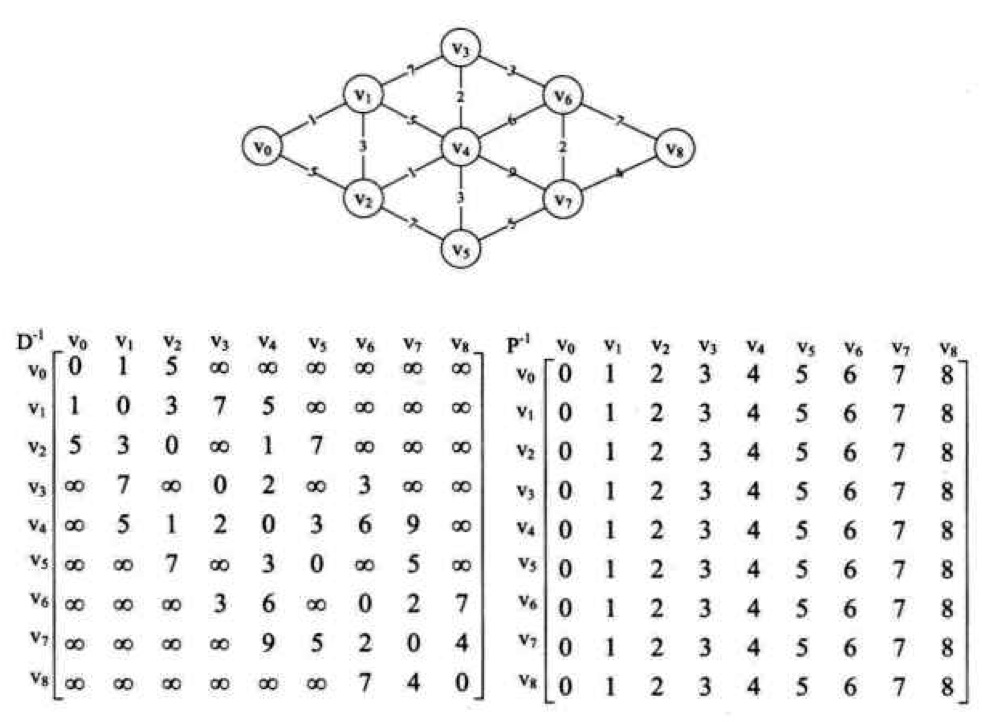
代碼


該算法用一個三層的循環遍歷了所有的頂點,并計算出了頂點與頂點之間的最短距離
其中: k代表中轉頂點、v代表起始點、w代表結束頂點
可以通過下面的圖形理解k,v,w是怎么運作的
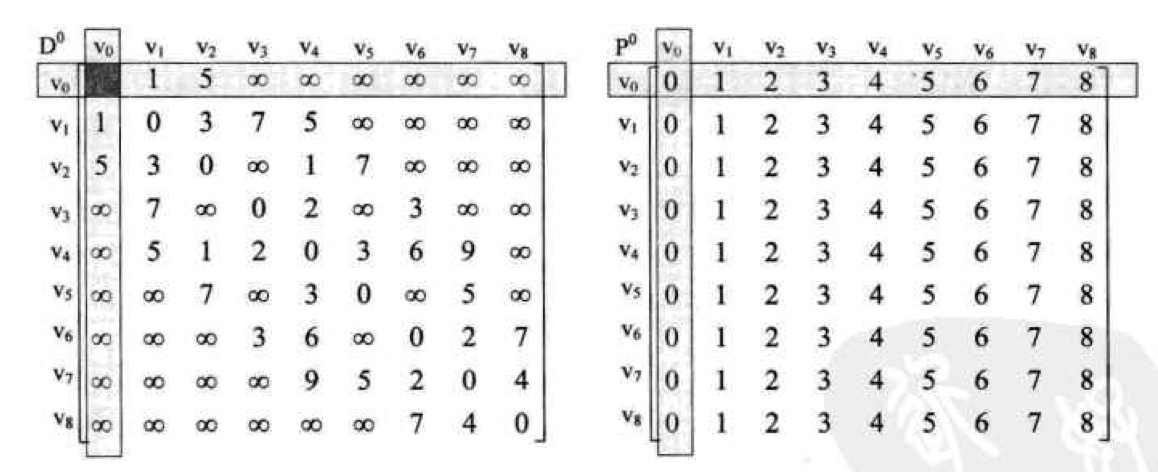
這是v0作為中轉頂點時,其他所有頂點通過它到結束點的最短路徑,發現不需要更新
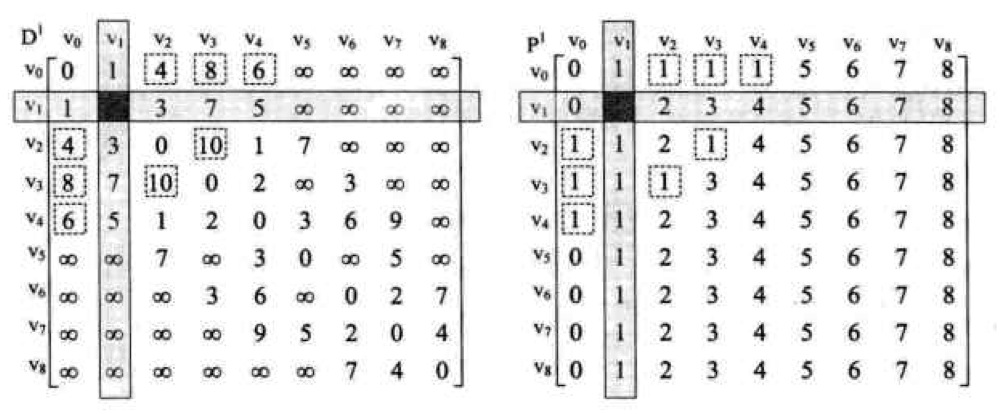
這是v1作為中轉頂點,可以看出,例如:原來v0->v2=5,而現在v0->v1->v2=1+3=4,因此我們就需要改變v0->v2的最短路徑為4,其他的同理。
就如同上面兩步一樣,循環進行直到所有頂點被處理一邊,最后結束得到的就是所有頂點到頂點之間的最短路徑