MNIST For ML Beginners

這個教程是給機器學習和TensorFlow的新手準備的，如果你已經知道MNIST是什么，softmax(多項式回歸)是什么，可以跳過。

當你開始學習編程時，可能第一件事就是打印'hello world'，機器學習與此類似的是MNIST。

MNIST是一個簡單的計算機視覺數據集，它由手寫的數字圖像組成

MNIST

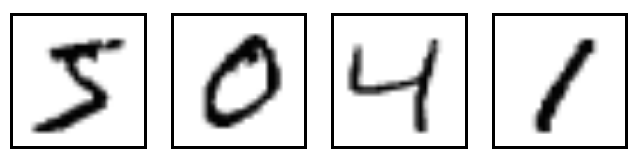
他也包含了每個圖像的標簽，告訴我們是什么數字，比如，上面4個圖像的標簽就是5,0,4,1.

在這個教程，我們將訓練一個根據圖形預測數字的模型。我們不是想訓練一個完美精確的模型，而是給TensorFlow做個初步教程。照此，我們用softmax回歸開始做一個簡單的模型。

這個教程的代碼非常短，而且真正值得注意的只有三行。但是，對于理解其背后的思想非常重要：TensorFlow怎樣工作的，機器學習的核心思想。

About this tutorial

這里的教程是逐行解釋mnist_softmax.py的代碼

你可以使用這里的代碼：

• 邊讀每一行的代碼解釋邊逐行復制粘貼到python環境中
• 運行整段代碼然后不清楚的地方再看教程

教程目的：

• 學習MNIST數據和softmax回歸
• 基于圖片像素的認知數字的函數創建
• 基于千計的樣本用TensorFlow訓練模型認知數字
• 用測試數據檢查模型的準確性

The MNIST Data

The MNIST Data存在于Yann LeCun's website,如果你復制粘貼這兩行代碼，它會自動下載讀取數據

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

MNIST被分割成三部分：55000個訓練集(mnist.train),10000個測試集(mnist.test),5000個驗證集(mnist.validation).這樣的分割是非常重要的：這樣我們可以確保模型的正確。

數據集中的每個樣本有兩部分：手寫數字的圖像和伴隨的標簽。我們稱圖像為x，標簽為y。訓練集和測試集都以此劃分，比如，訓練集的圖像是mnist.train.images,測試集的標簽是mnist.train.labels.

每個圖像是28*28的像素，我們可以理解為一個大的數字矩陣：

像素矩陣

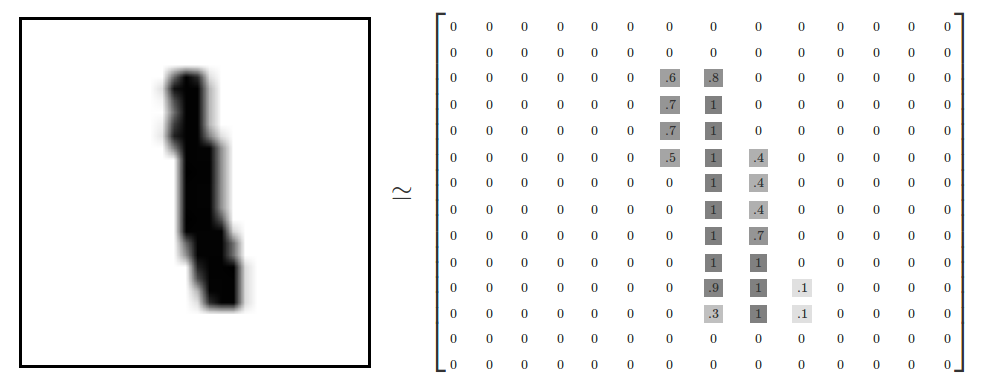
我們可以把這個矩陣平鋪成28*28=784個數字的向量。怎樣平鋪矩陣不重要，只要圖像之間保持一致就行了。按照這一觀點，MNIST圖像就是一個784維的向量空間(warning: computationally intensive visualizations).

平鋪2D結構的圖像會造成信息的丟棄。這是不好的嗎？最好的計算機視覺方法能夠利用這種2D結構，我們也將在之后的教程中介紹。但這里我們使用的softmax仍是使用的平鋪數據的方法。

mnist.train.images是形狀為[55000, 784]的張量。第一維是圖像列表的下標，第二維是每個圖像每個像素的下標。張量的每個元素是0到1之間的像素。

訓練數據的形式

MNIST的每個圖像都有一個伴隨的標簽，一個0到9之間的數字。

我們把我們的標簽當做'one-hot vectors'(獨熱編碼)。即大多維度是0，只有一個維度上是1，在這里，第n個數字的向量將在第n個維度上是1,3可以看成是[0,0,0,1,0,0,0,0,0,0].由此，mnist.train.labels即[55000,10]的浮點數矩陣。

獨熱編碼

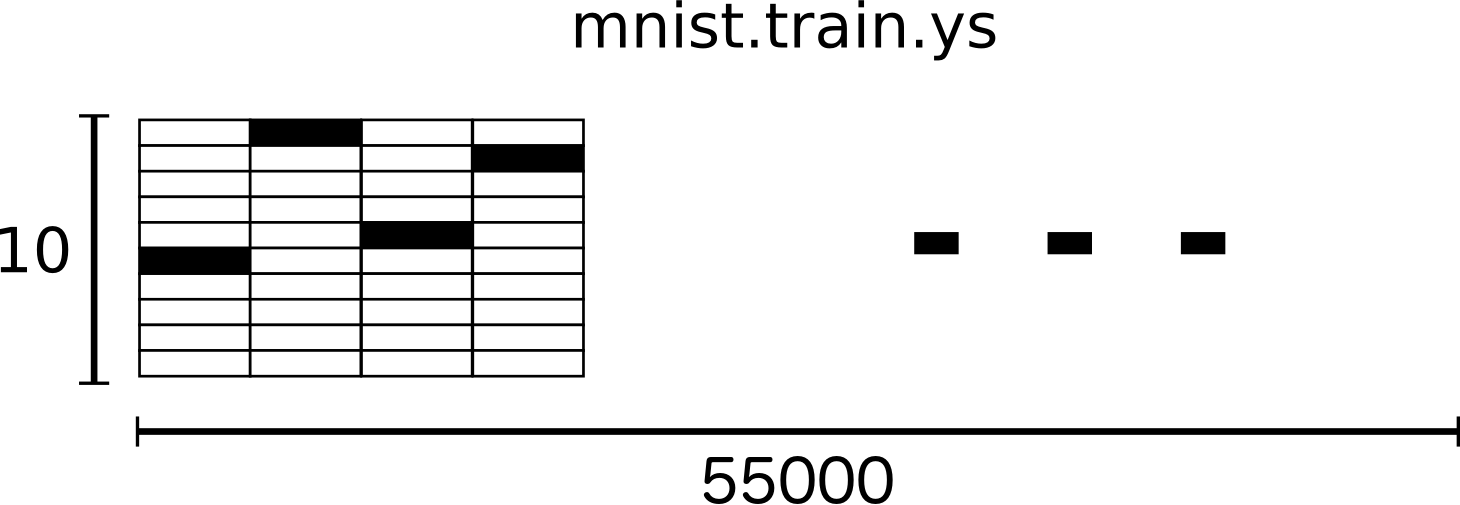
Softmax Regressions

我們知道mnist的每個圖像都是0到9的手寫數字。因此一個給出的圖像僅有10種可能。我們想要由一幅圖像給出它每個數字的概率，比如，看一張9的圖片，我們80%的概率確定是9,5%是8，其他數字概率更小。

softmax回歸是一種自然簡單的模型，如果你想要給一個多種可能的物體分配概率，softmax就是你需要的，因為softmax給我們一組0到1之間的序列，并且和為1.甚至之后，我們將訓練更復雜的模型，最后一步就是softmax層。

一個softmax回歸分為兩步：得到由輸入變成某一種類的證據，然后將證據轉換成概率。

為了得到給定圖片屬于某個特定數字的證據，我們對像素值加權求和，權重為負表示像素值有很強的證據不屬于該類，如果為正就支持證據。

下面的圖片顯示了一個模型學習到的圖片上每個像素對于特定數字類的權值。紅色代表負數權值，藍色代表正數權值。

圖片每個像素對于每個標簽的evidence

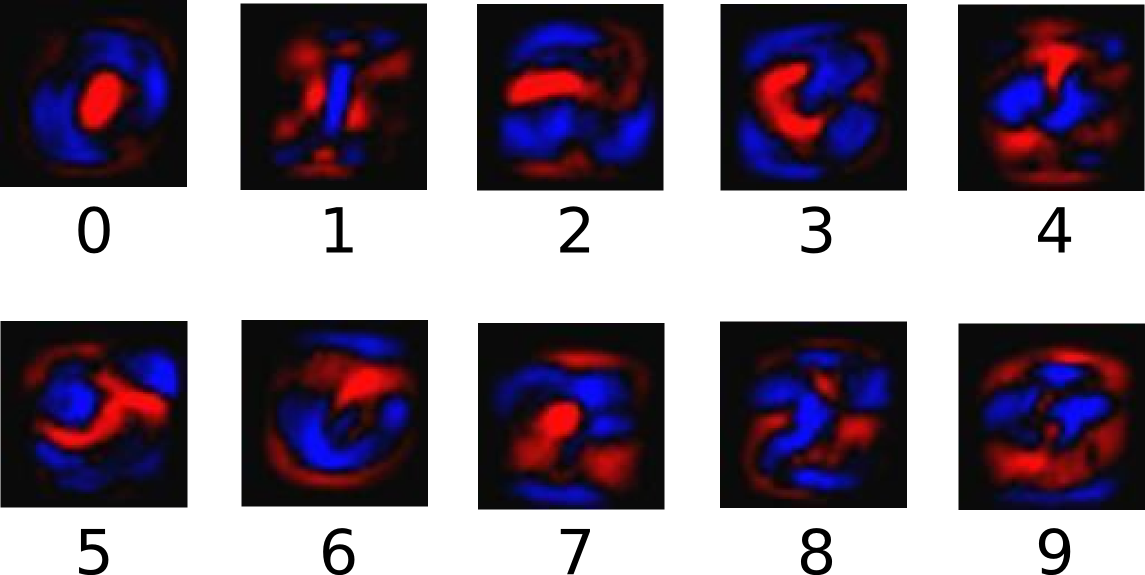
我們增加偏差作為額外的證據，因為輸入往往帶一些無關的干擾量，因此對于給定的輸入圖片 x 它代表的是數字 i 的證據可以表示為

1

其中W代表權重， b代表數字i類的偏置量，j代表給定圖片x的像素索引。然后用softmax函數可以把這些證據轉換成概率y

2

這里的softmax可以看做是activation(激勵)或link(鏈接)，把我們定義的線性函數的輸出轉換成我們想要的格式，也就是關于10個數字類的概率分布。因此，給定一張圖片，它對于每一個數字的吻合度可以被softmax函數轉換成為一個概率值。softmax函數可以定義為：

3

展開等式右邊的子式，可以得到：

4

但是更多的時候把softmax模型函數定義為前一種形式：把輸入值當成冪指數求值，再(normalize)歸一化這些結果值。這個冪運算表示，更大的證據對應更大的假設模型（hypothesis）里面的乘數權重值。反之，擁有更少的證據意味著在假設模型里面擁有更小的乘數系數。假設模型里的權值不可以是0值或者負值。Softmax然后會歸一化這些權重值，使它們的總和等于1，以此構造一個有效的概率分布。

你可以把softmax回歸看作下面的部分，對于每個輸出，我們對x加權求和，再加上一個偏置，再運用softmax。

softmax回歸

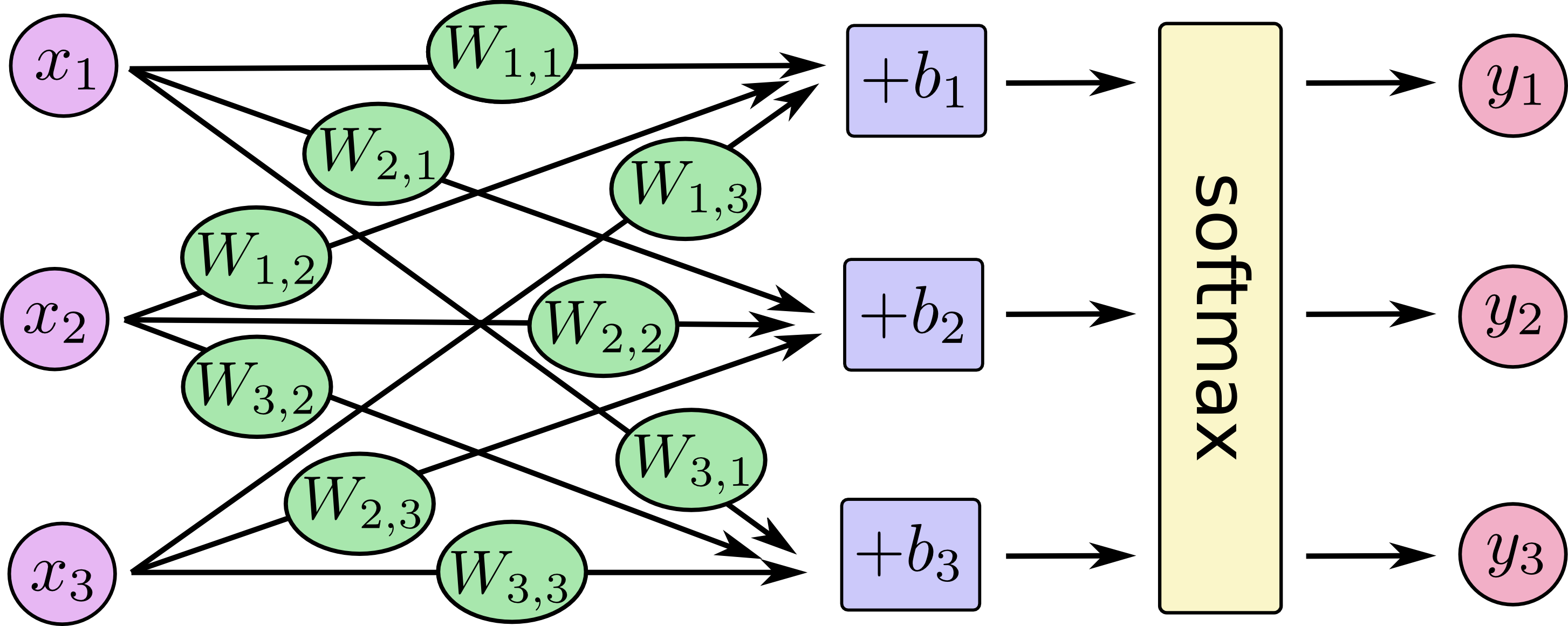
如果寫成一個等式，得到：

softmax回歸等式

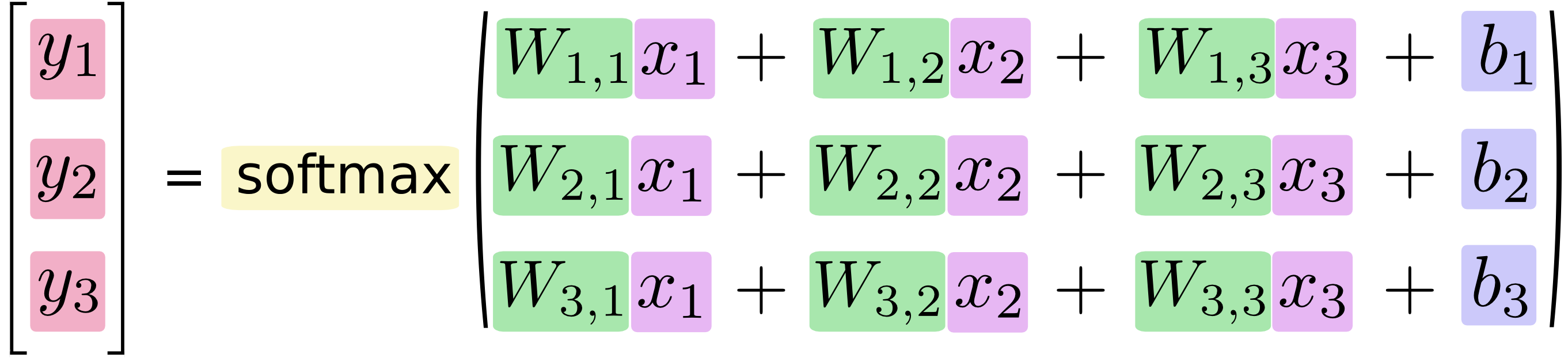
我們可以向量化這一結果，轉化成矩陣和向量的運算。有助于提高計算效率。

softmax回歸向量化等式

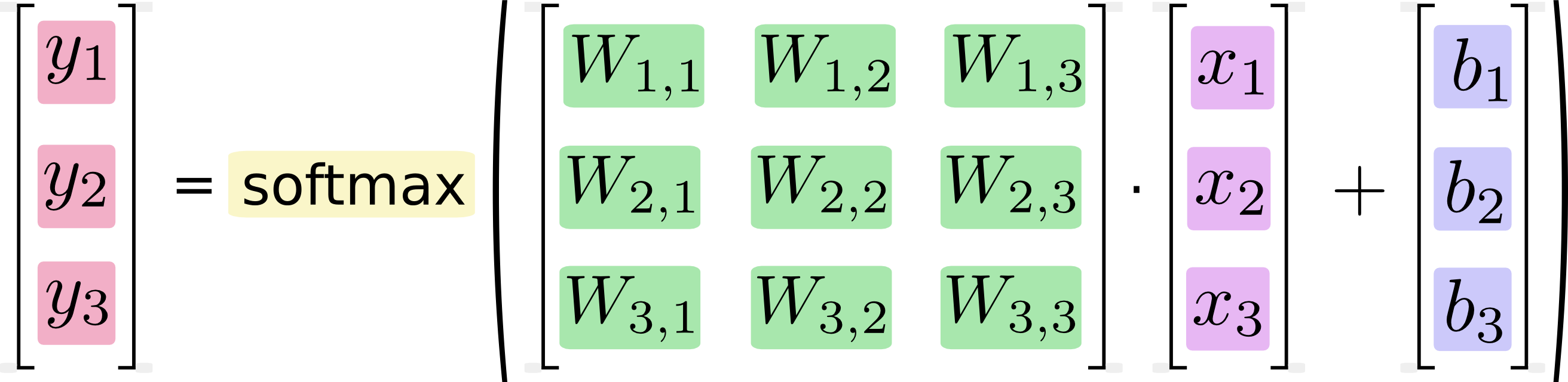
更進一步，可以寫成

5

現在我們把它轉化為TensorFlow可以使用的。

Implementing the Regression

為了用python實現高效的數值計算，我們通常會使用函數庫，比如NumPy，會把類似矩陣乘法這樣的復雜運算使用其他外部語言實現。不幸的是，從外部計算切換回Python的每一個操作，仍然是一個很大的開銷。如果你用GPU來進行外部計算，這樣的開銷會更大。用分布式的計算方式，也會花費更多的資源用來傳輸數據。

TensorFlow也把復雜的計算放在python之外完成，但是為了避免前面說的那些開銷，它做了進一步完善。Tensorflow不單獨地運行單一的復雜計算，而是讓我們可以先用圖描述一系列可交互的計算操作，然后全部一起在Python之外運行。（這樣類似的運行方式，可以在不少的機器學習庫中看到。）

使用TensorFlow之前，首先要導入它.import tensorflow as tf

我們通過操作符號化的變量來描述這些可交互的節點x = tf.placeholder(tf.float32, [None, 784])

x不是一個特定值，而是一個placeholder(占位符)。我們在TensorFlow運行計算時輸入這個值。我們希望能夠輸入任意數量的MNIST圖像，每一張圖展平成784維的向量。我們用2維的浮點數張量來表示這些圖，這個張量的形狀是[None，784 ]。（這里的None表示此張量的第一個維度可以是任何長度的。）

我們的模型也需要權重值和偏置量，當然我們可以把它們當做是額外的輸入，但TensorFlow有一個更好的方法來表示它們：Variable 。 一個Variable代表在計算圖交互節點中可修改的張量。它們可以在計算中使用和修改。對于機器學習，通常把模型參數視為變量。

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

我們用tf.Variable來得到變量的初始值來創建變量。在這里，我們把w和b初始化為0，既然要訓練w和b，就不用太在意初始值。

注意w的shape是[784,10]，因為我們想要用784維的圖片向量乘以它以得到一個10維的證據值向量，每一位對應不同數字類。b的形狀是[10]，所以我們可以直接把它加到輸出上面。

現在，我們可以實現我們的模型啦。只需要一行代碼！
y = tf.nn.softmax(tf.matmul(x, W) + b)
首先，我們用tf.matmul(??X，W)表示x乘以W，對應之前等式里面的，這里x是一個2維張量擁有多個輸入。然后再加上b，把和輸入到tf.nn.softmax函數里面。

至此，我們先用了幾行簡短的代碼來設置變量，然后只用了一行代碼來定義我們的模型。TensorFlow不僅僅可以使softmax回歸模型計算變得特別簡單，它也用這種非常靈活的方式來描述其他各種數值計算，從機器學習模型對物理學模擬仿真模型。一旦被定義好之后，我們的模型就可以在不同的設備上運行：計算機的CPU，GPU，甚至是手機！
訓練模型。

Training

為了訓練我們的模型，我們首先需要定義模型的好壞。其實，在機器學習，我們通常定義指標來表示一個模型是壞的，這個指標稱為成本（cost）或損失（loss），然后盡量最小化這個指標。也即是表征模型是好的。

一個常見的成本函數是“交叉熵”（cross-entropy）。交叉熵產生于信息論里面的信息壓縮編碼技術，但是它后來演變成為從博弈論到機器學習等其他領域里的重要技術手段。被定義為：

6

y 是我們預測的概率分布, y' 是實際的分布（我們輸入的one-hot vector)。比較粗糙的理解是，交叉熵是描述預測的低效性來描述真相。更詳細的關于交叉熵的解釋超出本教程的范疇，見understanding。

為了計算交叉熵，我們首先需要添加一個新的占位符用于輸入正確值：

y_ = tf.placeholder(tf.float32, [None, 10])

然后可以計算交叉熵：

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

首先，用 tf.log 計算 y 的每個元素的對數。接下來，我們把 y_ 的每一個元素和 tf.log(y) 的對應元素相乘。最后，用 tf.reduce_sum 計算張量的所有元素(第二個維度)的總和。最后，計算batch中所有樣本的均值。

在源代碼中，我們并沒有用這種格式，因為它常常數值不穩定。我們用tf.nn.softmax_cross_entropy_with_logits在未規范化的對數上(比如我們用softmax_cross_entropy_with_logits在tf.matmul(x, W) + b上)，這個函數計算softmax更加穩定。

現在我們知道我們需要我們的模型做什么啦，用TensorFlow來訓練它是非常容易的。因為TensorFlow得到了整個計算圖，它可以自動地使用反向傳播算法(backpropagation algorithm)來有效地確定你的變量是如何影響你想要最小化的那個成本值的。然后，TensorFlow會用你選擇的優化算法來不斷地修改變量以降低代價。

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

這里，我們用0.5學習率的gradient descent algorithm(梯度下降算法)來最小化交叉熵。梯度下降算法是一個簡單的學習過程，TensorFlow只需將每個變量一點點地往使代價不斷降低的方向移動。當然TensorFlow也提供了其他許多優化算法：只要簡單地調整一行代碼就可以使用其他的算法。

TensorFlow在這里實際上所做的是，在后臺給計算圖中增加一系列新的節點用于實現反向傳播算法和梯度下降算法。然后返回一個單一的節點，當運行這個操作時，它用梯度下降算法訓練你的模型，微調你的變量，不斷減少成本。

現在我們在InteractiveSession中啟動模型：

sess = tf.InteractiveSession()

首先，創建一個節點來初始化變量：

tf.global_variables_initializer().run()

讓模型循環訓練1000次：

for _ in range(1000):
  batch_xs, batch_ys = mnist.train.next_batch(100)
  sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

每一次循環中，從訓練集中隨機采樣100的數據點組成batch。賦值placeholder運行train_step。

使用隨機數據的batch來進行訓練被稱為隨機訓練（stochastic training）- 在這里更確切的說是隨機梯度下降訓練。在理想情況下，我們希望用我們所有的數據來進行每一步的訓練，因為這能給我們更好的訓練結果，但顯然這需要很大的計算開銷。所以，每一次訓練我們可以使用不同的數據子集，這樣做既可以減少計算開銷，又可以最大化地學習到數據集的總體特性。

Evaluating Our Model

那么我們的模型性能呢？

首先讓我們找出那些預測正確的標簽。tf.argmax 是一個非常有用的函數，它能給出某個tensor對象在某一維上的其數據最大值所在的索引值。由于標簽向量是由0,1組成，因此最大值1所在的索引位置就是類別標簽，比如tf.argmax(y,1)返回的是模型對于任一輸入x預測到的標簽值，而 tf.argmax(y_,1) 代表正確的標簽，我們可以用 tf.equal 來檢測我們的預測是否真實標簽匹配(索引位置一樣表示匹配)。

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

最后在測試集上驗證準確性

print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

大概是92%。

這是好的嗎？當然不那么好，事實上是相當差的。因為我們用的一個非常簡單的模型。做出一些改變，我們可以得到97%。最好的模型的可以達到99.7%(更多信息，可以看list of results)

重要的是我們從模型中學到的，如果你不滿足這個結果，可以看下一章節學習TensorFlow更多的模型。

附上mnist_softmax.py源代碼：

# Copyright 2015 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#     http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================

"""A very simple MNIST classifier.

See extensive documentation at
https://www.tensorflow.org/get_started/mnist/beginners
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys

from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

FLAGS = None


def main(_):
  # Import data
  mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)

  # Create the model
  x = tf.placeholder(tf.float32, [None, 784])
  W = tf.Variable(tf.zeros([784, 10]))
  b = tf.Variable(tf.zeros([10]))
  y = tf.matmul(x, W) + b

  # Define loss and optimizer
  y_ = tf.placeholder(tf.float32, [None, 10])

  # The raw formulation of cross-entropy,
  #
  #   tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(tf.nn.softmax(y)),
  #                                 reduction_indices=[1]))
  #
  # can be numerically unstable.
  #
  # So here we use tf.nn.softmax_cross_entropy_with_logits on the raw
  # outputs of 'y', and then average across the batch.
  cross_entropy = tf.reduce_mean(
      tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
  train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

  sess = tf.InteractiveSession()
  tf.global_variables_initializer().run()
  # Train
  for _ in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

  # Test trained model
  correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
  print(sess.run(accuracy, feed_dict={x: mnist.test.images,
                                      y_: mnist.test.labels}))

if __name__ == '__main__':
  parser = argparse.ArgumentParser()
  parser.add_argument('--data_dir', type=str, default='/tmp/tensorflow/mnist/input_data',
                      help='Directory for storing input data')
  FLAGS, unparsed = parser.parse_known_args()
  tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)