3.2 函數(shù)和所生成的過程

來源：3.2 Functions and the Processes They Generate

譯者：飛龍

協(xié)議：CC BY-NC-SA 4.0

函數(shù)是計算過程的局部演化模式。它規(guī)定了過程的每個階段如何構(gòu)建在之前的階段之上。我們希望能夠創(chuàng)建有關(guān)過程整體行為的語句，而過程的局部演化由一個或多個函數(shù)指定。這種分析通常非常困難，但是我們至少可以試圖描述一些典型的過程演化模式。

在這一章中，我們會檢測一些用于簡單函數(shù)所生成過程的通用“模型”。我們也會研究這些過程消耗重要的計算資源，例如時間和空間的比例。

3.2.1 遞歸函數(shù)

如果函數(shù)的函數(shù)體直接或者間接自己調(diào)用自己，那么這個函數(shù)是遞歸的。也就是說，遞歸函數(shù)的執(zhí)行過程可能需要再次調(diào)用這個函數(shù)。Python 中的遞歸函數(shù)不需要任何特殊的語法，但是它們的確需要一些注意來正確定義。

作為遞歸函數(shù)的介紹，我們以將英文單詞轉(zhuǎn)換為它的 Pig Latin 等價形式開始。Pig Latin 是一種隱語：對英文單詞使用一種簡單、確定的轉(zhuǎn)換來掩蓋單詞的含義。Thomas Jefferson 據(jù)推測是先行者。英文單詞的 Pig Latin 等價形式將輔音前綴（可能為空）從開頭移動到末尾，并且添加-ay元音。所以，pun會變成unpay，stout會變成outstay，all會變成allay。

>>> def pig_latin(w):
        """Return the Pig Latin equivalent of English word w."""
        if starts_with_a_vowel(w):
            return w + 'ay'
        return pig_latin(w[1:] + w[0])
>>> def starts_with_a_vowel(w):
        """Return whether w begins with a vowel."""
        return w[0].lower() in 'aeiou'

這個定義背后的想法是，一個以輔音開頭的字符串的 Pig Latin 變體和另一個字符串的 Pig Latin 變體相同：它通過將第一個字母移到末尾來創(chuàng)建。于是，sending的 Pig Latin 變體就和endings的變體（endingsay）相同。smother的 Pig Latin 變體和mothers的變體（othersmay）相同。而且，將輔音從開頭移動到末尾會產(chǎn)生帶有更少輔音前綴的更簡單的問題。在sending的例子中，將s移動到末尾會產(chǎn)生以元音開頭的單詞，我們的任務(wù)就完成了。

即使pig_latin函數(shù)在它的函數(shù)體中調(diào)用，pig_latin的定義是完整且正確的。

>>> pig_latin('pun')
'unpay'

能夠基于函數(shù)自身來定義函數(shù)的想法可能十分令人混亂：“循環(huán)”定義如何有意義，這看起來不是很清楚，更不用說讓計算機來執(zhí)行定義好的過程。但是，我們能夠準確理解遞歸函數(shù)如何使用我們的計算環(huán)境模型來成功調(diào)用。環(huán)境的圖示和描述pig_latin('pun')求值的表達式樹展示在下面：

Python 求值過程的步驟產(chǎn)生如下結(jié)果：

1. pig_latin的def語句 被執(zhí)行，其中：
   1. 使用函數(shù)體創(chuàng)建新的pig_latin函數(shù)對象，并且
   2. 將名稱pig_latin在當前（全局）幀中綁定到這個函數(shù)上。
2. starts_with_a_vowel的def語句類似地執(zhí)行。
3. 求出pig_latin('pun')的調(diào)用表達式，通過
   1. 求出運算符和操作數(shù)子表達式，通過
      1. 查找綁定到pig_latin函數(shù)的pig_latin名稱
      2. 對字符串對象'pun'求出操作數(shù)字符串字面值
   2. 在參數(shù)'pun'上調(diào)用pig_latin函數(shù)，通過
      1. 添加擴展自全局幀的局部幀
      2. 將形參w綁定到當前幀的實參'pun'上。
      3. 在以當前幀起始的環(huán)境中執(zhí)行pig_latin的函數(shù)體
         1. 最開始的條件語句沒有效果，因為頭部表達式求值為False
         2. 求出最后的返回表達式pig_latin(w[1:] + w[0])，通過
            1. 查找綁定到pig_latin函數(shù)的pig_latin名稱
            2. 對字符串對象'pun'求出操作數(shù)表達式
            3. 在參數(shù)'unp'上調(diào)用pig_latin，它會從pig_latin函數(shù)體中的條件語句組返回預(yù)期結(jié)果。

就像這個例子所展示的那樣，雖然遞歸函數(shù)具有循環(huán)特征，他仍舊正確調(diào)用。pig_latin函數(shù)調(diào)用了兩次，但是每次都帶有不同的參數(shù)。雖然第二個調(diào)用來自pig_latin自己的函數(shù)體，但由名稱查找函數(shù)會成功，因為名稱pig_latin在它的函數(shù)體執(zhí)行前的環(huán)境中綁定。

這個例子也展示了 Python 的遞歸函數(shù)的求值過程如何與遞歸函數(shù)交互，來產(chǎn)生帶有許多嵌套步驟的復(fù)雜計算過程，即使函數(shù)定義本身可能包含非常少的代碼行數(shù)。

3.2.2 剖析遞歸函數(shù)

許多遞歸函數(shù)的函數(shù)體中都存在通用模式。函數(shù)體以基本條件開始，它是一個條件語句，為需要處理的最簡單的輸入定義函數(shù)行為。在pig_latin的例子中，基本條件對任何以元音開頭的單詞成立。這個時候，只需要返回末尾附加ay的參數(shù)。一些遞歸函數(shù)會有多重基本條件。

基本條件之后是一個或多個遞歸調(diào)用。遞歸調(diào)用有特定的特征：它們必須簡化原始問題。在pig_latin的例子中，w中最開始輔音越多，就需要越多的處理工作。在遞歸調(diào)用pig_latin(w[1:] + w[0])中，我們在一個具有更少初始輔音的單詞上調(diào)用pig_latin -- 這就是更簡化的問題。每個成功的pig_latin調(diào)用都會更加簡化，直到滿足了基本條件：一個沒有初始輔音的單詞。

遞歸調(diào)用通過逐步簡化問題來表達計算。與我們在過去使用過的迭代方式相比，它們通常以不同方式來解決問題。考慮用于計算n的階乘的函數(shù)fact，其中fact(4)計算了4! = 4·3·2·1 = 24。

使用while語句的自然實現(xiàn)會通過將每個截至n的正數(shù)相乘來求出結(jié)果。

>>> def fact_iter(n):
        total, k = 1, 1
        while k <= n:
            total, k = total * k, k + 1
        return total
>>> fact_iter(4)
24

另一方面，階乘的遞歸實現(xiàn)可以以fact(n-1)（一個更簡單的問題）來表示fact(n)。遞歸的基本條件是問題的最簡形式：fact(1)是1。

>>> def fact(n):
        if n == 1:
            return 1
        return n * fact(n-1)
>>> fact(4)
24

函數(shù)的正確性可以輕易通過階乘函數(shù)的標準數(shù)學(xué)定義來驗證。

(n ? 1)! = (n ? 1)·(n ? 2)· ... · 1
n！ = n·(n ? 1)·(n ? 2)· ... · 1
n! = n·(n ? 1)!  

這兩個階乘函數(shù)在概念上不同。迭代的函數(shù)通過將每個式子，從基本條件1到最終的總數(shù)逐步相乘來構(gòu)造結(jié)果。另一方面，遞歸函數(shù)直接從最終的式子n和簡化的問題fact(n-1)構(gòu)造結(jié)果。

將fact函數(shù)應(yīng)用于更簡單的問題實例，來展開遞歸的同時，結(jié)果最終由基本條件構(gòu)建。下面的圖示展示了遞歸如何向fact傳入1而終止，以及每個調(diào)用的結(jié)果如何依賴于下一個調(diào)用，直到滿足了基本條件。

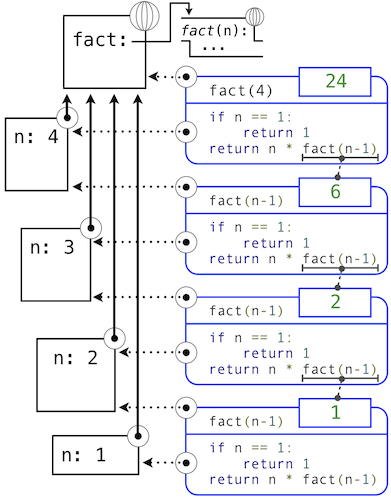
雖然我們可以使用我們的計算模型展開遞歸，通常把遞歸調(diào)用看做函數(shù)抽象更清晰一些。也就是說，我們不應(yīng)該關(guān)心fact(n-1)如何在fact的函數(shù)體中實現(xiàn)；我們只需要相信它計算了n-1的階乘。將遞歸調(diào)用看做函數(shù)抽象叫做遞歸的“信仰飛躍”（leap of faith）。我們以函數(shù)自身來定義函數(shù)，但是僅僅相信更簡單的情況在驗證函數(shù)正確性時會正常工作。這個例子中我們相信，fact(n-1)會正確計算(n-1)!；我們只需要檢查，如果滿足假設(shè)n!是否正確計算。這樣，遞歸函數(shù)正確性的驗證就變成了一種歸納證明。

函數(shù)fact_iter和fact也不一樣，因為前者必須引入兩個額外的名稱，total和k，它們在遞歸實現(xiàn)中并不需要。通常，迭代函數(shù)必須維護一些局部狀態(tài)，它們會在計算過程中改變。在任何迭代的時間點上，狀態(tài)刻畫了已完成的結(jié)果，以及未完成的工作總量。例如，當k為3且total為2時，就還剩下兩個式子沒有處理，3和4。另一方面，fact由單一參數(shù)n來刻畫。計算的狀態(tài)完全包含在表達式樹的結(jié)果中，它的返回值起到total的作用，并且在不同的幀中將n綁定到不同的值上，而不是顯式跟蹤k。

遞歸函數(shù)可以更加依賴于解釋器本身，通過將計算狀態(tài)儲存為表達式樹和環(huán)境的一部分，而不是顯式使用局部幀中的名稱。出于這個原因，遞歸函數(shù)通常易于定義，因為我們不需要試著弄清必須在迭代中維護的局部狀態(tài)。另一方面，學(xué)會弄清由遞歸函數(shù)實現(xiàn)的計算過程，需要一些練習(xí)。

3.2.3 樹形遞歸

另一個遞歸的普遍模式叫做樹形遞歸。例如，考慮斐波那契序列的計算，其中每個數(shù)值都是前兩個的和。

>>> def fib(n):
        if n == 1:
            return 0
        if n == 2:
            return 1
        return fib(n-2) + fib(n-1)
>>> fib(6)
5

這個遞歸定義和我們之前的嘗試有很大關(guān)系：它準確反映了斐波那契數(shù)的相似定義。考慮求出fib(6)所產(chǎn)生的計算模式，它展示在下面。為了計算fib(6)，我們需要計算fib(5)和fib(4)。為了計算fib(5)，我們需要計算fib(4)和fib(3)。通常，這個演化過程看起來像一棵樹（下面的圖并不是完整的表達式樹，而是簡化的過程描述；一個完整的表達式樹也擁有同樣的結(jié)構(gòu)）。在遍歷這棵樹的過程中，每個藍點都表示斐波那契數(shù)的已完成計算。

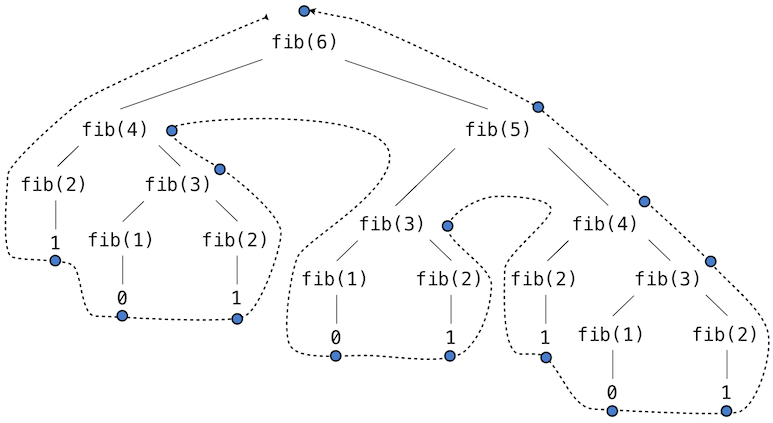
調(diào)用自身多次的函數(shù)叫做樹形遞歸。以樹形遞歸為原型編寫的函數(shù)十分有用，但是用于計算斐波那契數(shù)則非常糟糕，因為它做了很多重復(fù)的計算。要注意整個fib(4)的計算是重復(fù)的，它幾乎是一半的工作量。實際上，不難得出函數(shù)用于計算fib(1)和fib(2)（通常是樹中的葉子數(shù)量）的時間是fib(n+1)。為了弄清楚這有多糟糕，我們可以證明fib(n)的值隨著n以指數(shù)方式增長。所以，這個過程的步驟數(shù)量隨輸入以指數(shù)方式增長。

我們已經(jīng)見過斐波那契數(shù)的迭代實現(xiàn)，出于便利在這里貼出來：

>>> def fib_iter(n):
        prev, curr = 1, 0  # curr is the first Fibonacci number.
        for _ in range(n-1):
             prev, curr = curr, prev + curr
        return curr

這里我們必須維護的狀態(tài)由當前值和上一個斐波那契數(shù)組成。for語句也顯式跟蹤了迭代數(shù)量。這個定義并沒有像遞歸方式那樣清晰反映斐波那契數(shù)的數(shù)學(xué)定義。但是，迭代實現(xiàn)中所需的計算總數(shù)只是線性，而不是指數(shù)于n的。甚至對于n的較小值，這個差異都非常大。

然而我們不應(yīng)該從這個差異總結(jié)出，樹形遞歸的過程是沒有用的。當我們考慮層次數(shù)據(jù)結(jié)構(gòu)，而不是數(shù)值上的操作時，我們發(fā)現(xiàn)樹形遞歸是自然而強大的工具。而且，樹形過程可以變得更高效。

記憶。用于提升重復(fù)計算的遞歸函數(shù)效率的機制叫做記憶。記憶函數(shù)會為任何之前接受的參數(shù)儲存返回值。fib(4)的第二次調(diào)用不會執(zhí)行與第一次同樣的復(fù)雜過程，而是直接返回第一次調(diào)用的已儲存結(jié)果。

記憶函數(shù)可以自然表達為高階函數(shù)，也可以用作裝飾器。下面的定義為之前的已計算結(jié)果創(chuàng)建緩存，由被計算的參數(shù)索引。在這個實現(xiàn)中，這個字典的使用需要記憶函數(shù)的參數(shù)是不可變的。

>>> def memo(f):
        """Return a memoized version of single-argument function f."""
        cache = {}
        def memoized(n):
            if n not in cache:
                cache[n] = f(n)
            return cache[n]
        return memoized
>>> fib = memo(fib)
>>> fib(40)
63245986

由記憶函數(shù)節(jié)省的所需的計算時間總數(shù)在這個例子中是巨大的。被記憶的遞歸函數(shù)fib和迭代函數(shù)fib_iter都只需要線性于輸入n的時間總數(shù)。為了計算fib(40)，fib的函數(shù)體只執(zhí)行 40 次，而不是無記憶遞歸中的 102,334,155 次。

空間。為了理解函數(shù)所需的空間，我們必須在我們的計算模型中規(guī)定內(nèi)存如何使用，保留和回收。在求解表達式過程中，我們必須保留所有活動環(huán)境和所有這些環(huán)境引用的值和幀。如果環(huán)境為表達式樹當前分支中的一些表達式提供求值上下文，那么它就是活動環(huán)境。

例如，當求值fib時，解釋器按序計算之前的每個值，遍歷樹形結(jié)構(gòu)。為了這樣做，它只需要在計算的任何時間點，跟蹤樹中在當前節(jié)點之前的那些節(jié)點。用于求出剩余節(jié)點的內(nèi)存可以被回收，因為它不會影響未來的計算。通常，樹形遞歸所需空間與樹的深度成正比。

下面的圖示描述了由求解fib(3)生成的表達式樹。在求解fib最初調(diào)用的返回表達式的過程中，fib(n-2)被求值，產(chǎn)生值0。一旦這個值計算出來，對應(yīng)的環(huán)境幀（標為灰色）就不再需要了：它并不是活動環(huán)境的一部分。所以，一個設(shè)計良好的解釋器會回收用于儲存這個幀的內(nèi)存。另一方面，如果解釋器當前正在求解fib(n-1)，那么由這次fib調(diào)用（其中n為2）創(chuàng)建的環(huán)境是活動的。與之對應(yīng)，最開始在3上調(diào)用fib所創(chuàng)建的環(huán)境也是活動的，因為這個值還沒有成功計算出來。

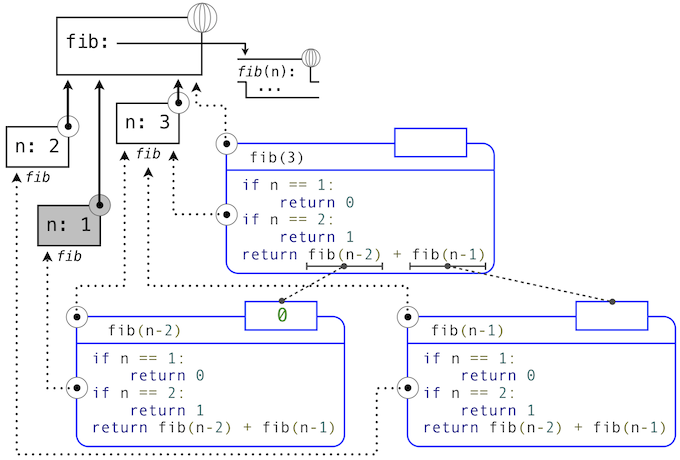
在memo的例子中，只要一些名稱綁定到了活動環(huán)境中的某個函數(shù)上，關(guān)聯(lián)到所返回函數(shù)（它包含cache）的環(huán)境必須保留。cache字典中的條目數(shù)量隨傳遞給fib的唯一參數(shù)數(shù)量線性增長，它的規(guī)模線性于輸入。另一方面，迭代實現(xiàn)只需要兩個數(shù)值來在計算過程中跟蹤：prev和curr，所以是常數(shù)大小。

我們使用記憶函數(shù)的例子展示了編程中的通用模式，即通常可以通過增加所用空間來減少計算時間，反之亦然。

3.2.4 示例：找零

考慮下面這個問題：如果給你半美元、四分之一美元、十美分、五美分和一美分，一美元有多少種找零的方式？更通常來說，我們能不能編寫一個函數(shù)，使用一系列貨幣的面額，計算有多少種方式為給定的金額總數(shù)找零？

這個問題可以用遞歸函數(shù)簡單解決。假設(shè)我們認為可用的硬幣類型以某種順序排列，假設(shè)從大到小排列。

使用n種硬幣找零的方式為：

1. 使用所有除了第一種之外的硬幣為a找零的方式，以及
2. 使用n種硬幣為更小的金額a - d找零的方式，其中d是第一種硬幣的面額。

為了弄清楚為什么這是正確的，可以看出，找零方式可以分為兩組，不使用第一種硬幣的方式，和使用它們的方式。所以，找零方式的總數(shù)等于不使用第一種硬幣為該金額找零的方式數(shù)量，加上使用第一種硬幣至少一次的方式數(shù)量。而后者的數(shù)量等于在使用第一種硬幣之后，為剩余的金額找零的方式數(shù)量。

因此，我們可以遞歸將給定金額的找零問題，歸約為使用更少種類的硬幣為更小的金額找零的問題。仔細考慮這個歸約原則，并且說服自己，如果我們規(guī)定了下列基本條件，我們就可以使用它來描述算法：

1. 如果a正好是零，那么有一種找零方式。
2. 如果a小于零，那么有零種找零方式。
3. 如果n小于零，那么有零種找零方式。

我們可以輕易將這個描述翻譯成遞歸函數(shù)：

>>> def count_change(a, kinds=(50, 25, 10, 5, 1)):
        """Return the number of ways to change amount a using coin kinds."""
        if a == 0:
            return 1
        if a < 0 or len(kinds) == 0:
            return 0
        d = kinds[0]
        return count_change(a, kinds[1:]) + count_change(a - d, kinds)
>>> count_change(100)
292

count_change函數(shù)生成樹形遞歸過程，和fib的首個實現(xiàn)一樣，它是重復(fù)的。它會花費很長時間來計算出292，除非我們記憶這個函數(shù)。另一方面，設(shè)計迭代算法來計算出結(jié)果的方式并不是那么明顯，我們將它留做一個挑戰(zhàn)。

3.2.5 增長度

前面的例子表明，不同過程在花費的時間和空間計算資源上有顯著差異。我們用于描述這個差異的便捷方式，就是使用增長度的概念，來獲得當輸入變得更大時，過程所需資源的大致度量。

令n為度量問題規(guī)模的參數(shù)，R(n)為處理規(guī)模為n的問題的過程所需的資源總數(shù)。在我們前面的例子中，我們將n看做給定函數(shù)所要計算出的數(shù)值。但是還有其他可能。例如，如果我們的目標是計算某個數(shù)值的平方根近似值，我們會將n看做所需的有效位數(shù)的數(shù)量。通常，有一些問題相關(guān)的特性可用于分析給定的過程。與之相似，R(n)可用于度量所用的內(nèi)存總數(shù)，所執(zhí)行的基本的機器操作數(shù)量，以及其它。在一次只執(zhí)行固定數(shù)量操作的計算中，用于求解表達式的所需時間，與求值過程中執(zhí)行的基本機器操作數(shù)量成正比。

我們說，R(n)具有Θ(f(n))的增長度，寫作R(n)=Θ(f(n))（讀作“theta f(n)”），如果存在獨立于n的常數(shù)k1和k2，那么對于任何足夠大的n值：

k1·f(n) <= R(n) <= k2·f(n)

也就是說，對于較大的n，R(n)的值夾在兩個具有f(n)規(guī)模的值之間：

• 下界k1·f(n)，以及
• 上界k2·f(n)。

例如，計算n!所需的步驟數(shù)量與n成正比，所以這個過程的所需步驟以Θ(n)增長。我們也看到了，遞歸實現(xiàn)fact的所需空間以Θ(n)增長。與之相反，迭代實現(xiàn)fact_iter花費相似的步驟數(shù)量，但是所需的空間保持不變。這里，我們說這個空間以Θ(1)增長。

我們的樹形遞歸的斐波那契數(shù)計算函數(shù)fib的步驟數(shù)量，隨輸入n指數(shù)增長。尤其是，我們可以發(fā)現(xiàn)，第 n 個斐波那契數(shù)是距離φ^(n-2)/√5的最近整數(shù)，其中φ是黃金比例：

φ = (1 + √5)/2 ≈ 1.6180

我們也表示，步驟數(shù)量隨返回值增長而增長，所以樹形遞歸過程需要Θ(φ^n)的步驟，它的一個隨n指數(shù)增長的函數(shù)。

增長度只提供了過程行為的大致描述。例如，需要n^2個步驟的過程和需要1000·n^2個步驟的過程，以及需要3·n^2+10·n+17個步驟的過程都擁有Θ(n^2)的增長度。在特定的情況下，增長度的分析過于粗略，不能在函數(shù)的兩個可能實現(xiàn)中做出判斷。

但是，增長度提供了實用的方法，來表示在改變問題規(guī)模的時候，我們應(yīng)如何預(yù)期過程行為的改變。對于Θ(n)（線性）的過程，使規(guī)模加倍只會使所需的資源總數(shù)加倍。對于指數(shù)的過程，每一點問題規(guī)模的增長都會使所用資源以固定因數(shù)翻倍。接下來的例子展示了一個增長度為對數(shù)的算法，所以使問題規(guī)模加倍，只會使所需資源以固定總數(shù)增加。

3.2.6 示例：求冪

考慮對給定數(shù)值求冪的問題。我們希望有一個函數(shù)，它接受底數(shù)b和正整數(shù)指數(shù)n作為參數(shù)，并計算出b^n。一種方式就是通過遞歸定義：

b^n = b·b^(n-1)
b^0 = 1

這可以翻譯成遞歸函數(shù)：

>>> def exp(b, n):
        if n == 0:
            return 1
        return b * exp(b, n-1)

這是個線性的遞歸過程，需要Θ(n)的步驟和空間。就像階乘那樣，我們可以編寫等價的線性迭代形式，它需要相似的步驟數(shù)量，但只需要固定的空間。

>>> def exp_iter(b, n):
        result = 1
        for _ in range(n):
            result = result * b
        return result

我們可以以更少的步驟求冪，通過逐次平方。例如，我們這樣計算b^8：

b·(b·(b·(b·(b·(b·(b·b))))))

我們可以使用三次乘法來計算它：

b^2 = b·b
b^4 = b^2·b^2
b^8 = b^4·b^4

這個方法對于 2 的冪的指數(shù)工作良好。我們也可以使用這個遞歸規(guī)則，在求冪中利用逐步平方的優(yōu)點：

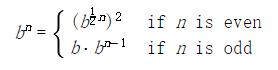
我們同樣可以將這個方式表達為遞歸函數(shù)：

>>> def square(x):
        return x*x
>>> def fast_exp(b, n):
        if n == 0:
            return 1
        if n % 2 == 0:
            return square(fast_exp(b, n//2))
        else:
            return b * fast_exp(b, n-1)
>>> fast_exp(2, 100)
1267650600228229401496703205376

fast_exp所生成的過程的空間和步驟數(shù)量隨n以對數(shù)方式增長。為了弄清楚它，可以看出，使用fast_exp計算b^2n比計算b^n只需要一步額外的乘法操作。于是，我們能夠計算的指數(shù)大小，在每次新的乘法操作時都會（近似）加倍。所以，計算n的指數(shù)所需乘法操作的數(shù)量，增長得像以2為底n的對數(shù)那樣慢。這個過程擁有Θ(log n)的增長度。Θ(log n)和Θ(n)之間的差異在n非常大時變得顯著。例如，n為1000時，fast_exp僅僅需要14個乘法操作，而不是1000。