
在深入研究機器學習與深度學習之前我們需要了解一些基本概念,機器學習中的很多公式就是從這些基本概念和基本公式中推演發展出來的。同時我們還需要掌握基本的微積分和線性代數的知識,越到后面,公式的推演愈加復雜。
<h4>假設函數(The Hypothesis Function)</h4>
假設我們有一堆輸入項:
以及輸出項:
假設存在一個線性函數
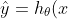=\theta_0 + \theta_1\cdot x)
能夠精確地擬合這些輸入項與輸出項,那么這樣的函數被稱為假設函數(在統計學里可以被稱為回歸線吧)
假設我們有以下的訓練集:
| inuput | output |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 6 |
| 3 | 7 |
此時,我們假設第一個參數為1,第二個參數為2,則我們的假設函數為:
當輸入值為2時,預測的輸出值為5,但是實際值為6,因此我們嘗試不同的參數組合來找出最為擬合這些訓練集的假設函數。為了度量假設函數與訓練集之間的誤差,我們提出代價函數(cost function)的概念。
<h4> 代價函數(Cost Function)</h4>
我們可以用統計學中方差的概念來理解代價函數
這個公式實際上就是統計學中的方差公式,其代價函數的值越小,則假設函數與訓練集擬合得越好,在以后的學習中,我們需要常常用到這個公式。
<h4>梯度下降算法(Gradient Descent Algorithm)</h4>
梯度下降算法是一種用來計算代價函數局部極小值的一種算法,在之后的研究中,梯度下降算法是一個大殺器。
由于假設函數是其參數
的函數(為方便討論,我們暫時只考慮僅含有兩個參數的hypothesis function),因此我們通過不斷地修改這兩個參數使我們的假設函數愈加地擬合我們的數據集,也就是說我們不斷地使這兩個參數的代價函數值越來越小。假設我們將cost function以這兩個參數為自變量,其值為因變量繪制三維圖,我們假設cost function的函數圖像如下圖所示:

假設圖中小球所處的位置即我們在cost function上任意選擇的一處位置,微積分的知識告訴我們,圖中的小球會隨著曲面的梯度不斷下降(其梯度也在不斷地變化),直到其下降到曲面的最低點。但是這個算法所算得的最小值很可能是曲面的局部最小值,關于這個問題的探討可以在維基百科里看到。(傳送門)
微積分的知識告訴我們,代價函數J關于這兩個參數的梯度為:
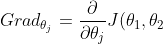,j=1,2)
因此其參數的變化可以這樣表示:
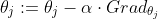
其參數α代表的是梯度下降的速率,因為計算機無法處理連續變化的值,因此我們只能用一些列變化較小的離散量來表示連續變化的值。
<h4>總結</h4>
以上就是入門機器學習及深度學習需要掌握的一些基礎知識,想了解更多的話可以參考我寫的構建神經網絡來識別手寫數字,或者Andrew Ng的線上課程:機器學習。