前言：

以斯坦福cs231n課程的python編程任務(wù)為主線，展開對該課程主要內(nèi)容的理解和部分?jǐn)?shù)學(xué)推導(dǎo)。該課程相關(guān)筆記參考自知乎-CS231n官方筆記授權(quán)翻譯總集篇發(fā)布課程材料和事例參考自-cs231n
本章為線性分類器的softmax講解，緊接上章的SVM，其中涉及到的一些線性分類器的知識已經(jīng)在上章說明，本次便不再贅述。cs231n課程作業(yè)assignment1（SVM）

SoftMax分類器簡介：

Softmax和SVM同屬于線性分類器，主要的區(qū)別在于Softmax的損失函數(shù)與SVM的損失函數(shù)的不同。Softmax分類器就可以理解為邏輯回歸分類器面對多個分類的一般化歸納。SVM將輸出f(x_i,W)作為每個分類的評分，而Softmax的輸出的是評分所占的比重，這樣顯得更加直觀。

在Softmax分類器中，函數(shù)映射f(x_i;W)=Wx_i保持不變，但將這些評分值視為每個分類的未歸一化的對數(shù)概率，并且將折葉損失（hinge loss）替換為交叉熵?fù)p失（cross-entropy loss）。公式如下：

)
或

在上式中，使用f_j來表示分類評分向量中f的第j個元素個,數(shù)據(jù)集的損失值是數(shù)據(jù)集中所有樣本數(shù)據(jù)的損失值的均值與正則化損失R(W)之和。其中Softmax函數(shù)為:

 = \frac{e^{{z_j}}{\sum_ke}{f_j}})

其輸入值是一個向量，向量中元素為任意實數(shù)的評分值（z中的），函數(shù)對其進行壓縮，輸出一個向量，其中每個元素值在0到1之間，且所有元素之和為1。

除了損失函數(shù)不同，其他的操作與SVM基本相同，進一步的講，SVM分類器使用的是折葉損失（hinge loss），而Softmax使用的是交叉熵?fù)p失（corss-entropy loss），本質(zhì)上都屬于線性分類器的一種。

Softmax與SVM比較:

img

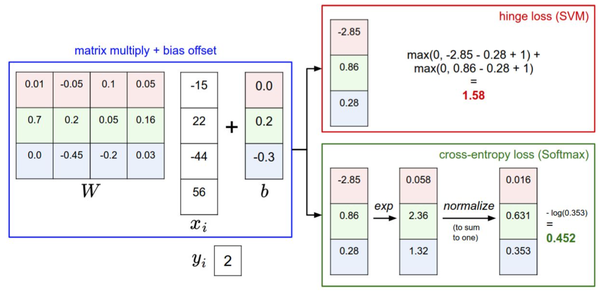
針對一個數(shù)據(jù)點，SVM和Softmax分類器的不同處理方式的例子。兩個分類器都計算了同樣的分值。不同之處在于對$f$分值的解釋：SVM分類器將它們看做是分類評分，它的損失函數(shù)鼓勵正確的分類（本例中是藍色的類別2）的分值比其他分類的分值高出至少一個邊界值。Softmax分類器將這些數(shù)值看做是每個分類沒有歸一化的對數(shù)概率，鼓勵正確分類的歸一化的對數(shù)概率變高，其余的變低。SVM的最終的損失值是1.58，Softmax的最終的損失值是0.452，但要注意這兩個數(shù)值沒有可比性。只在給定同樣數(shù)據(jù)，在同樣的分類器的損失值計算中，它們才有意義。

在實際使用中，SVM和Softmax經(jīng)常是相似的：通常說來，兩種分類器的表現(xiàn)差別很小，不同的人對于哪個分類器更好有不同的看法。相對于Softmax分類器，SVM更加“局部目標(biāo)化（local objective）”，這既可以看做是一個特性，也可以看做是一個劣勢。考慮一個評分是[10, -2, 3]的數(shù)據(jù)，其中第一個分類是正確的。那么一個SVM（&$Delta =1$)會看到正確分類相較于不正確分類，已經(jīng)得到了比邊界值還要高的分?jǐn)?shù)，它就會認(rèn)為損失值是0。SVM對于數(shù)字個體的細(xì)節(jié)是不關(guān)心的：如果分?jǐn)?shù)是[10, -100, -100]或者[10, 9, 9]，對于SVM來說沒設(shè)么不同，只要滿足超過邊界值等于1，那么損失值就等于0。

對于softmax分類器，情況則不同。對于[10, 9, 9]來說，計算出的損失值就遠(yuǎn)遠(yuǎn)高于[10, -100, -100]的。換句話來說，softmax分類器對于分?jǐn)?shù)是永遠(yuǎn)不會滿意的：正確分類總能得到更高的可能性，錯誤分類總能得到更低的可能性，損失值總是能夠更小。但是，SVM只要邊界值被滿足了就滿意了，不會超過限制去細(xì)微地操作具體分?jǐn)?shù)。這可以被看做是SVM的一種特性。舉例說來，一個汽車的分類器應(yīng)該把他的大量精力放在如何分辨小轎車和大卡車上，而不應(yīng)該糾結(jié)于如何與青蛙進行區(qū)分，因為區(qū)分青蛙得到的評分已經(jīng)足夠低了。

Softmax實現(xiàn)：

<li>softmax.py

    import numpy as np
    from random import shuffle
    import math
    
    def softmax_loss_naive(W, X, y, reg):
      """
      Softmax loss function, naive implementation (with loops)
    
      Inputs have dimension D, there are C classes, and we operate on minibatches
      of N examples.
    
      Inputs:
      - W: A numpy array of shape (D, C) containing weights.
      - X: A numpy array of shape (N, D) containing a minibatch of data.
      - y: A numpy array of shape (N,) containing training labels; y[i] = c means
        that X[i] has label c, where 0 <= c < C.
      - reg: (float) regularization strength
    
      Returns a tuple of:
      - loss as single float
      - gradient with respect to weights W; an array of same shape as W
      """
      # Initialize the loss and gradient to zero.
      loss = 0.0
      dW = np.zeros_like(W)
      num_classes = W.shape[1]
      num_train = X.shape[0]
      loss = 0.0
      for i in xrange(num_train):
        scores = X[i].dot(W)
        scores = np.exp(scores)
        scores = normalized(scores)
        for j in xrange(num_classes):
          if j == y[i]:
            continue
          margin = -np.log(scores_correct)
          if margin > 0:
            loss += margin
            dW[:, y[i]] += -X[i, :]    
            dW[:, j] += X[i, :]         
    
      # Right now the loss is a sum over all training examples, but we want it
      # to be an average instead so we divide by num_train.
      loss /= num_train
      dW /= num_train
      # Add regularization to the loss.
      dW += reg * W
     
      return loss, dW
    
    
    def softmax_loss_vectorized(W, X, y, reg):
      """
      Softmax loss function, vectorized version.
    
      Inputs and outputs are the same as softmax_loss_naive.
      """
      # Initialize the loss and gradient to zero.
      loss = 0.0
      dW = np.zeros_like(W)
      scores = X.dot(W) 
      scores = np.exp(scores) 
      scores = normalized(scores)
      num_classes = W.shape[1]
      num_train = X.shape[0]
    
      margins = -np.log(scores)
      ve_sum = np.sum(margins,axis=1)/num_classes
      y_trueClass = np.zeros_like(margins)
      y_trueClass[range(num_train), y] = 1.0
      loss += (np.sum(ve_sum) / num_train)
      dW += np.dot(X.T,scores-y_trueClass)/num_train
    
      return loss, dW
    
    def normalized(a):
        sum_scores =  np.sum(a,axis=1)
        sum_scores =  1 / sum_scores
        result = a.T * sum_scores.T
        return result.T

測試：

不同參數(shù)下Softmax的識別率結(jié)果：

softmax

總結(jié)：

本章主要介紹了另一個線性分類器Softmax，闡述了Softmax與SVM的主要區(qū)別，而Softmax的loss function對于以后的神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)有很大的幫助。