---

layout:? ? post

title:? ? ? Andrew Ng Stanford機器學(xué)習(xí)公開課 總結(jié)（5）

subtitle:? Lecture 5 高斯判別分析和樸素貝葉斯

date:? ? ? 2019-07-19

author:? ? ZhangWenXiang

header-img: img/post-bg-cook.jpg

catalog: true

tags:

? ? - 機器學(xué)習(xí)

? ? - Andrew Ng 吳恩達 Stanford 機器學(xué)習(xí)公開課

? ? - Gaussian Discriminant Analysis

? ? - Generative Learning

? ? - Naive Bayes

---

# Lecture 5 高斯判別分析和樸素貝葉斯

介紹Gaussian Discriminant Analysis以及Naive Bayes

## 生成式學(xué)習(xí) Generative Learning algorithm

>關(guān)鍵詞：Generative vs Discriminative

### 判別式算法 Discriminative learning algorithm

如邏輯回歸、決策樹、SVM等常見算法都是直接對p(y|x;θ)進行建模，這類算法叫做判別式發(fā)算法(Discriminative learning algorithm)。以二分類的邏輯回歸為例，對于給定的一組動物的特征數(shù)據(jù)，需要我們對數(shù)據(jù)進行分類：y=1代表大象、y=0代表狗。那么分類算法（如lr）要做的就是找到一個決策邊界（在一維空間就是一條線），之后對于一條數(shù)據(jù)，根據(jù)該數(shù)據(jù)在決策邊界的哪一邊，來判斷該動物是狗還是大象。

Discriminative learning algorithm的重點在于找到一個映射mapping，從x->y的映射，這樣可以根據(jù)特征x判斷類別y。

### 生成式學(xué)習(xí) Generative Learning algorithm

生成式算法與判別式算法相反，首先給出根據(jù)一群大象，之后算法對大象的特征分布建模，即學(xué)習(xí)大象長什么樣。同理，給我們一群狗，算法對狗的特征分布進行建模。因此，實際上生成式算法是對p(x|y;θ)建模。因此，p(x|y = 0)表示狗的特征分布，p(x|y = 1)表示大象的特征分布。

那么，那么用特征分布來對樣本分類呢，答案是貝葉斯定理（Bayes rule）。根據(jù)貝葉斯rule：


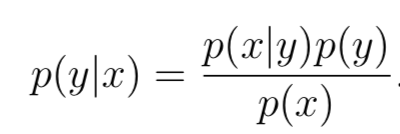
其中p(y)叫做先驗分布（class priors），根據(jù)概率公式不難得出p(x) = p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)，但其實預(yù)測分類的時候，根本用不到p(x)，因為對于某個樣本來說，不非是比較p(y=0|x)和p(y=1|x)的大小，根據(jù)大小判斷樣本所屬類別，其中p(x)是比較項的公共分母，因此可以直接去掉，不影響大小關(guān)系。用公式表達就是：


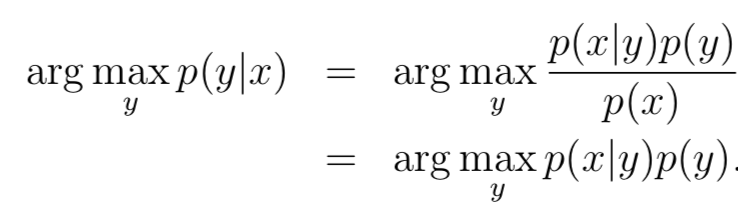
## 1.? 高斯判別分析 Gaussian discriminant analysis

Gaussian discrim- inant analysis (GDA)高斯判別分析就是生成式算法的一種。GDA假設(shè)p(x|y)服從多元正態(tài)分布。

### 1.1? 多元正態(tài)分布 The multivariate normal distribution

多元正態(tài)分布也叫多元高斯分布multivariate Gaussian distribution，對于n-dimendions的多元高斯分布 參數(shù)為：均值向量 μ ∈ Rn 以及協(xié)方差矩陣 Σ ∈ Rn×n, 其中 Σ ≥ 0 即半正定。因此N(μ, Σ)的概率密度為：


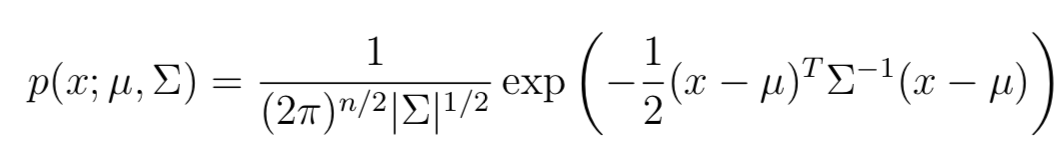
其中，|Σ|代表矩陣Σ的行列式。對于服從N(μ, Σ)分布的隨機變量X，均值μ為：


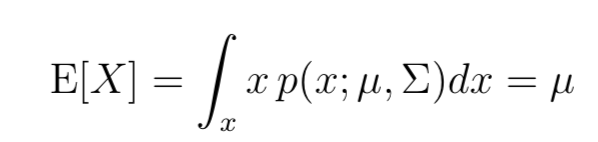
在概率論中，協(xié)方差公式可以表示為:


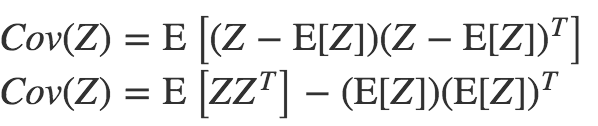
因此，對于任意 X ～ N (μ, Σ)必然能夠推導(dǎo)出Cov(X) = Σ。

以上是對于公式的基本解釋，下面利用圖像加深理解：二維(2-dimension)的高斯分布


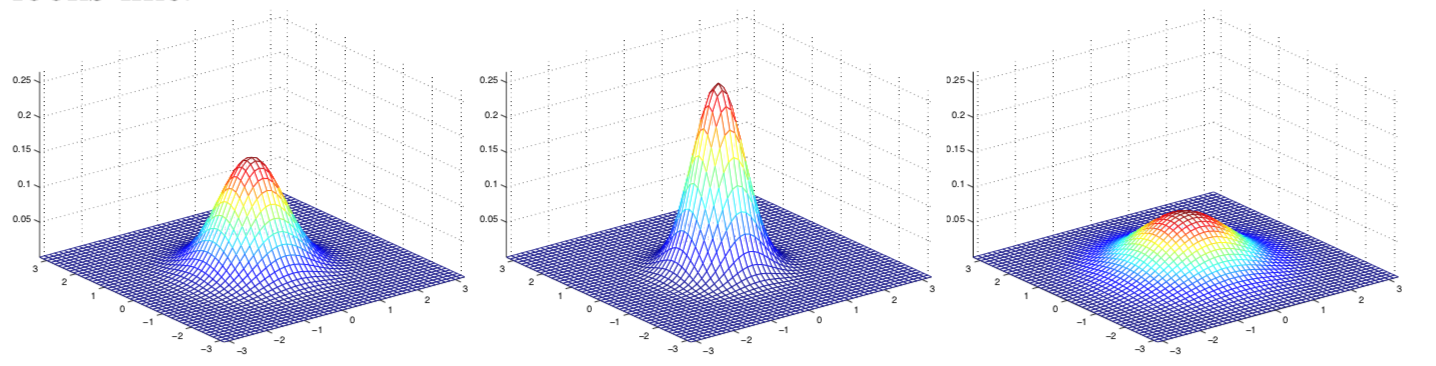
因為是二維的高斯，因此均值μ是2*1的向量，而協(xié)方差Σ是2*2的矩陣。其中最左邊的是**標準正態(tài)分布**，也就是μ=[0,0] 0均值, Σ=I=[[1,1],[1,1]]單位矩陣；中間的依舊是0均值，但是Σ = 0.6I；最右側(cè)的Σ = 2I。因此不難看出，隨著Σ變大 高斯分布變得更矮更胖(spread-out and compressed)。具體分布例子，可以參考原講義。

### 1.2? 高斯判別分析模型 The Gaussian Discriminant Analysis model

對于分類問題，y∈{0,1}代表標簽，隨機變量x代表輸入特征，利用GDA對p(x|y)建模：


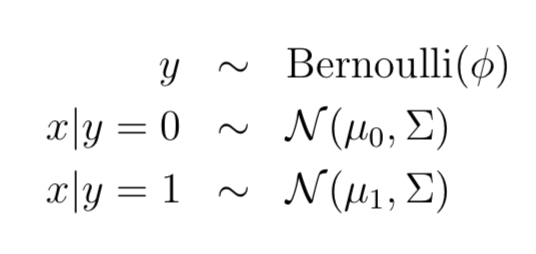
其中標簽y∈{0,1}因此服從伯努利(Bernoulli)分布，對于y給定的情況下，條件概率p(x|y=0 or 1)服從高斯分布，這就是GDA的基本假設(shè)。更詳細的分布公式如下：


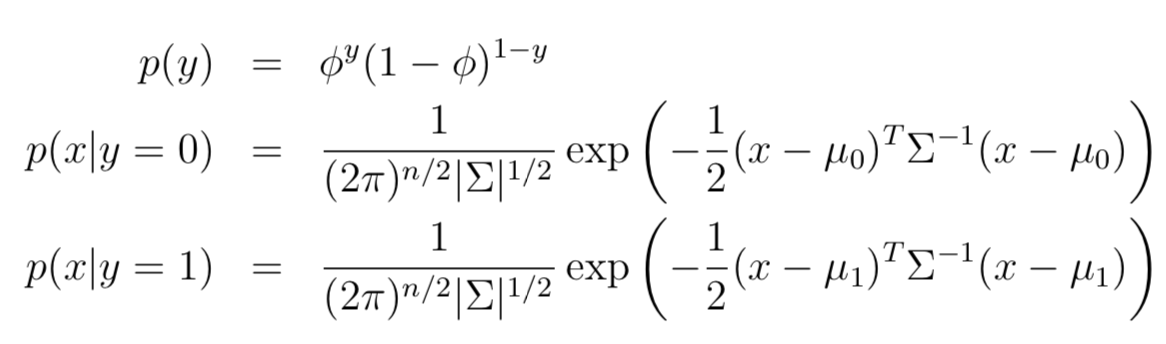
>通常情況下，模型采用兩個均值向量μ0 和 μ1，但是協(xié)方差矩陣采用同一個Σ。

模型參數(shù)包括：φ, Σ, μ0, μ1。φ表示y=1的概率，那么(1-φ)表示y=0的概率。因此 log似然函數(shù)(log-likelihood)為：


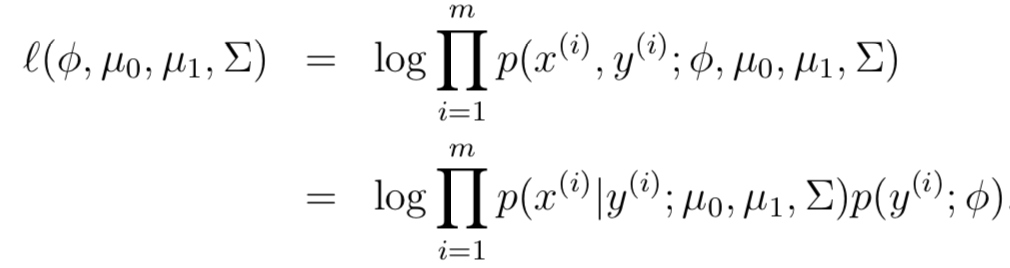
通過最大化似然估計，可以推導(dǎo)出各個參數(shù)的估計為：這里只給出結(jié)果，如果想了解具體推導(dǎo)過程，請參考[博客](https://www.cnblogs.com/jcchen1987/p/4424436.html)。


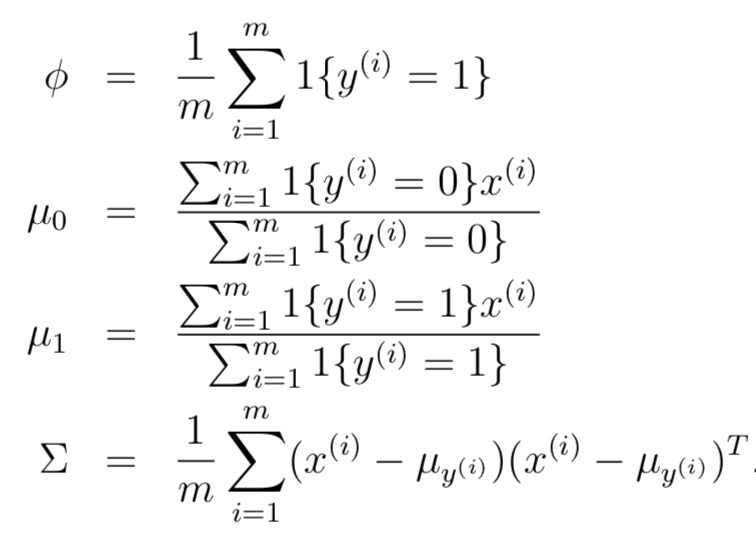
為了更好的直觀理解，請看下圖：


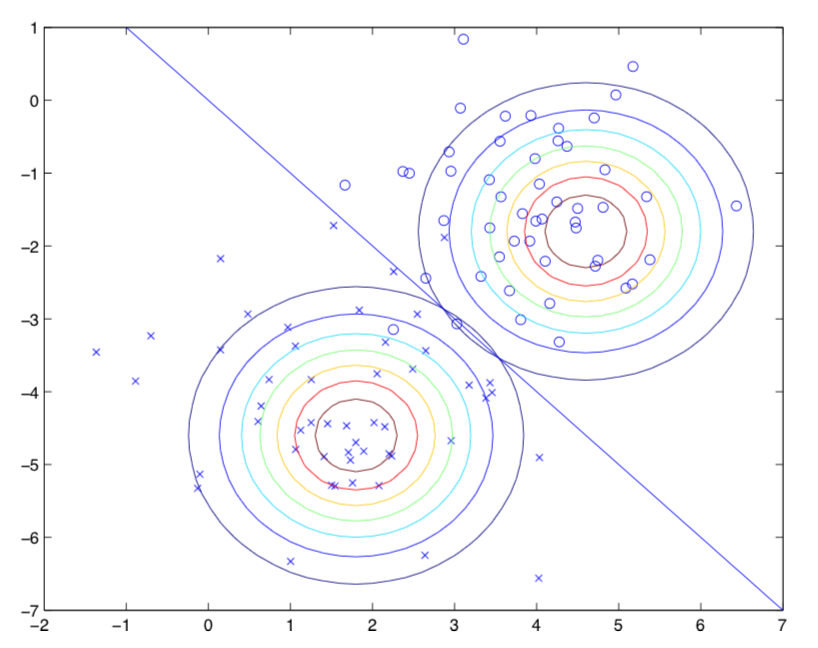
圖中圓圈代表正樣本，叉號代表負樣本，直線p(y = 1|x) = 0.5代表分類邊界(decision boundary)。因為Σ相同所以兩個形狀相同，但是具有不同的μ 。

### 1.3? 高斯判別分析 VS 邏輯回歸

>邏輯回歸LR請參考我的另一篇[文章](https://github.com/Demmon-tju/spark-ml-source-mark/blob/master/ml/classification/logistic%20regression/Logistic%20Regression%20邏輯回歸.md)

首先說結(jié)論：對于GDA的概率分布p(y = 1|x; φ, μ0, μ1, Σ)，如果將其看作針對變量x的函數(shù)的話，那么p可以表示成邏輯函數(shù)的形式：其中θ是φ,Σ,μ0,μ1的函數(shù)。


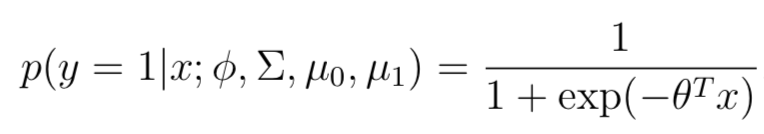
與LR的形式完全一樣，但是這個形式是怎么來的呢：根據(jù)上文p(x|y=1)和p(x|y=0)服從**相同協(xié)方差**的**高斯分布**，可以得到如下推導(dǎo)


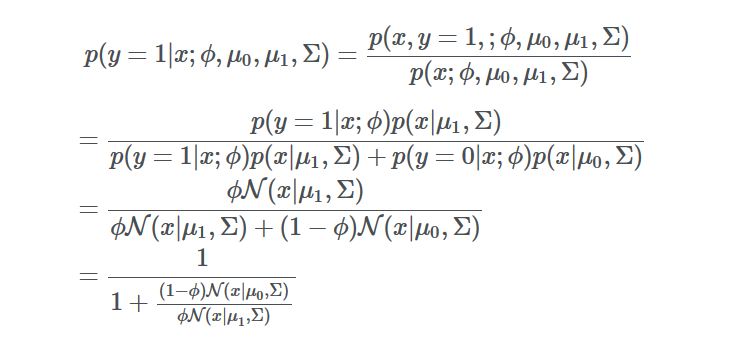
由于高斯分布屬于指族，因此公式下面的比例部分可以轉(zhuǎn)化成 exp(θTx)的形式，其中θ是φ,Σ,μ0,μ1的函數(shù)。

>結(jié)論：如果p(x|y)服從多元高斯分布(相同Σ)，那么p(y|x)就一定是邏輯函數(shù)；其實對于x|y服從泊松分布，即p(x|y=0) ～ Poisson(λ0), p(x|y=1) ～ Poisson(λ1)，同樣可以得出p(y|x)是邏輯函數(shù)。但是反過來都是不成立的，也就是y|x服從邏輯分布，并不能得出x的分布是高斯還是柏松。

因此，GDA和LR的區(qū)別為：

- GDA帶有更強的假設(shè)，對數(shù)據(jù)要求更高，因為要求數(shù)據(jù)服從高斯分布。而LR更加普世，不在乎數(shù)據(jù)的分布，不論是數(shù)據(jù)服從高斯還是柏松，LR都可以得到很好的結(jié)果。當然，如果數(shù)據(jù)確實服從多元高斯分布，那么GDA效果會更加好。

- 同時GDA需要的數(shù)據(jù)量也要遠小于LR，少量數(shù)據(jù)就可以得到不錯的結(jié)果。

- 工業(yè)界LR更為常用，因為不用考慮x的分布，同時LR更加簡單，具有較好的解釋性。

------

## 2.? 樸素貝葉斯 Naive Bayes

### 2.1.? 介紹

上文的GDA，特征x是連續(xù)向量。而對于離散值的特征，顯然無法利用高斯分布的假設(shè)，那么GDA也就無從談起。這時Naive Bayes(NB)就應(yīng)運而生了。

首先考慮一個郵件分類的例子：一封email會包含很多單詞，這些單詞就是特征，我們要做的就是對郵件進行分類，y=1代表垃圾郵件，y=0代表正常郵件。那么問題來了，特征x到底怎么表示呢，一種通用的方法就是one-hot，如下：


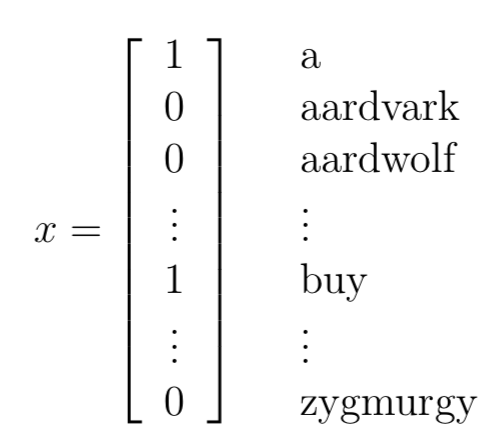
向量的長度就是詞表的大小，值表示該單詞是否在該郵件中出現(xiàn)過，1表示出現(xiàn)過。如果詞表大小是5000，那么x就是5000-dimensional的{0,1}向量。對于生成式模型，我們必須對p(x|y)建模，如果利用多項式分布(multinomial distribution)對x建模，那么參數(shù)規(guī)模為(2^50000 ?1)-dimensional參數(shù)向量。顯然參數(shù)規(guī)模太大。因此NB提出了一個樸素貝葉斯假設(shè)(Naive Bayes assumption)來解決這個問題。

### 2.2.? 模型

>條件獨立假設(shè)：給定y的情況下，x1和x2是獨立的，即p(x1|y) = p(x1|y, x2)。注意與p(x1) = p(x1|x2)不同，這表示任何情況都獨立。與NB假設(shè)不一樣，尤其注意。

條件獨立假設(shè)的直觀解釋就是，例如buy是詞表中第2087個詞，第price是詞表中第39831個詞，那么如果給定我們y=1也就是這是個垃圾郵件的情況下，是否出現(xiàn)buy與是否出現(xiàn)price是獨立的，即 p(x2087|y) = p(x2087|y, x39831)。根據(jù)條件獨立假設(shè)，那么公式可以改寫成：


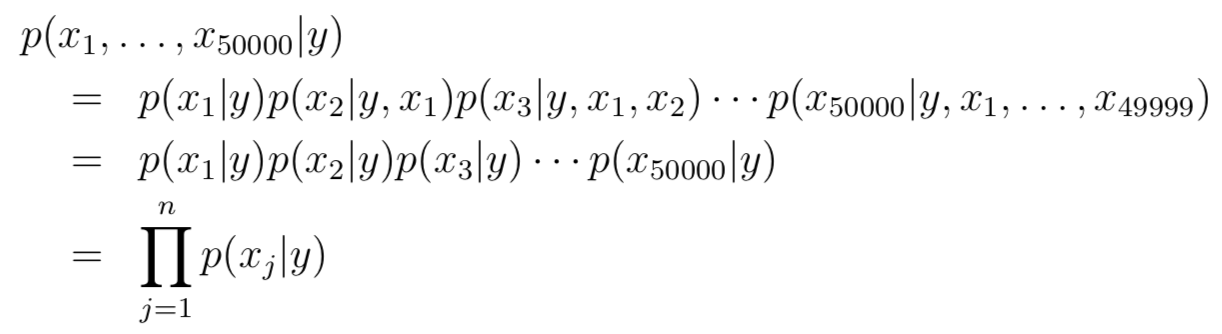
其實這個假設(shè)在多數(shù)情況下是不成立的，但是真是應(yīng)用中，即便假設(shè)不成立，但是NB模型依舊可以取得不錯效果。我們將模型參數(shù)簡化表示為：

- φj|y=1 = p(xj = 1|y = 1)

- φj|y=0 = p(xj = 1|y = 0)

- and φy = p(y = 1)

給定m個訓(xùn)練樣本，那么樣本表示為：{(x(i),y(i));i = 1, . . . , m}，因此似然函數(shù)如下：


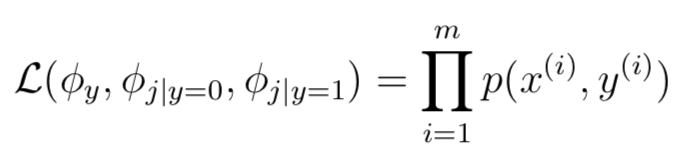
最大化上述函數(shù)，可以得出如下結(jié)果：只給出結(jié)果，推導(dǎo)過程并不難


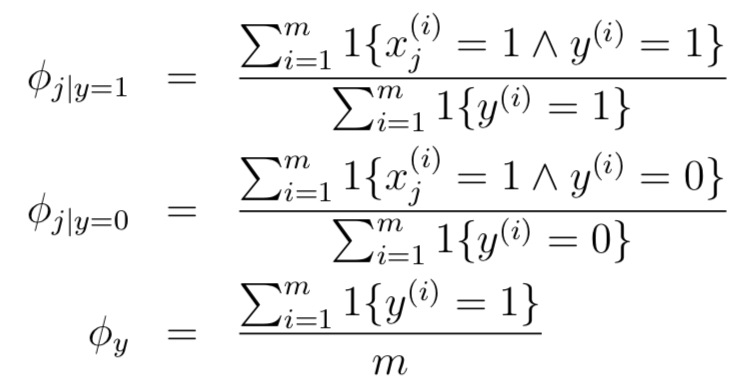
公式中的“∧”代表“且”。上述結(jié)果符合我們的直觀理解：φj|y=1就是垃圾郵件中詞語j出現(xiàn)的比例，φj|y=0同理，φy就是樣本中垃圾郵件的比例。

### 2.3.? 預(yù)測

對于給定一個特征x，怎樣預(yù)測y=0還是1呢？答案就是貝葉斯公式，與GDA類似，計算給定x的情況下，y=1的概率大小：


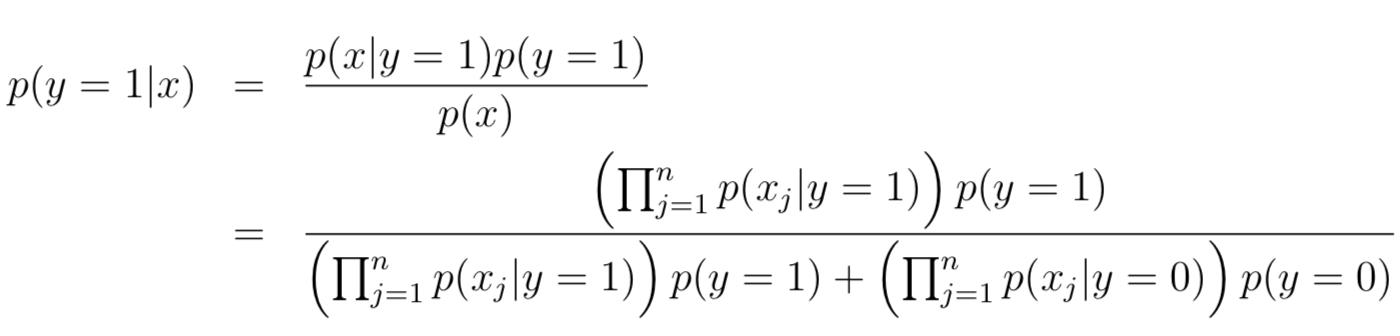
對于連續(xù)值，我們也可以先將其離散化，之后采用NB的方法。

### 2.4.? 拉普拉斯平滑 Laplace smoothing

如果詞語在我們之前的訓(xùn)練樣本中沒有出現(xiàn)過，那么p(x=|y=0)和p(x=|y=1)都等于0，因此計算p(y|x)=0/0，無法計算。Laplace smoothing目的就是解決這個問題，因此公式有所變化：



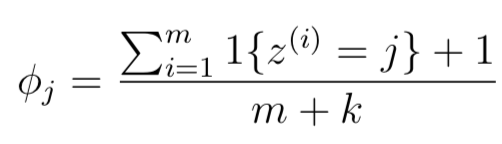
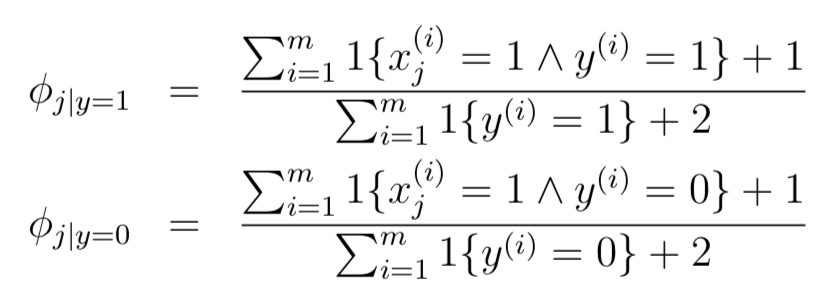
### 參考

- [GDA數(shù)學(xué)推導(dǎo)](https://www.cnblogs.com/jcchen1987/p/4424436.html)

- [網(wǎng)易公開課](http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record )

- [課程主頁](http://cs229.stanford.edu/)

- [課程筆記](https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes2.pdf)