2.2 監(jiān)督學(xué)習(xí) II

原文：Machine Learning for Humans, Part 2.1: Supervised Learning

作者：Vishal Maini

譯者：飛龍

協(xié)議：CC BY-NC-SA 4.0

使用對數(shù)幾率回歸（LR）和支持向量機(jī)（SVM）的分類。

分類：預(yù)測標(biāo)簽

這個郵件是不是垃圾郵件？貸款者能否償還它們的貸款？用戶是否會點擊廣告？你的 Fackbook 照片中那個人是誰？

分類預(yù)測離散的目標(biāo)標(biāo)簽Y。分類是一種問題，將新的觀測值分配給它們最有可能屬于的類，基于從帶標(biāo)簽的訓(xùn)練集中構(gòu)建的模型。

你的分類的準(zhǔn)確性取決于所選的算法的有效性，你應(yīng)用它的方式，以及你有多少有用的訓(xùn)練數(shù)據(jù)。

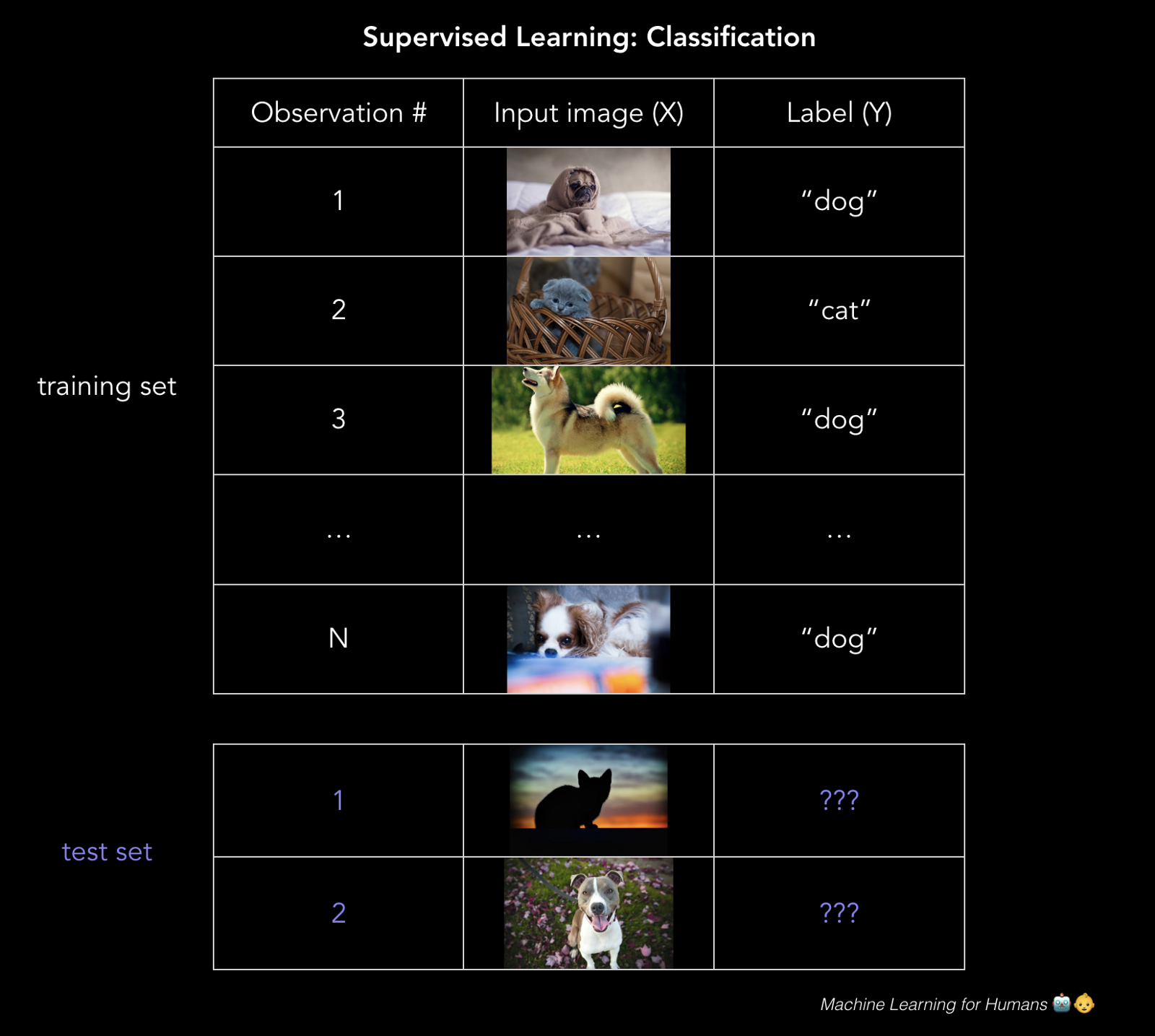
對數(shù)幾率回歸：0 還是 1？

對數(shù)幾率（logistic）回歸是個分類方法：模型輸出目標(biāo)變量Y屬于某個特定類的概率。

分類的一個很好的例子是，判斷貸款申請人是不是騙子。

最終，出借人想要知道，它們是否應(yīng)該貸給借款人，以及它們擁有一些容忍度，用于抵抗申請人的確是騙子的風(fēng)險。這里，對數(shù)幾率回歸的目標(biāo)就是計算申請人是騙子的概率（0%~100%）。使用這些概率，我們可以設(shè)定一些閾值，我們愿意借給高于它的借款人，對于低于它的借款人，我們拒絕他們的貸款申請，或者標(biāo)記它們以便后續(xù)觀察。

雖然對數(shù)幾率回歸通常用于二元分類，其中只存在兩個類，要注意，分類可以擁有任意數(shù)量的類（例如，為手寫數(shù)字分配 0~9 的標(biāo)簽，或者使用人臉識別來檢測 Fackbook 圖片中是哪個朋友）。

我可以使用普通最小二乘嘛？

不能。如果你在大量樣本上訓(xùn)練線性回歸模型，其中Y = 0或者1，你最后可能預(yù)測出一些小于 0 或者大于 1 的概率，這毫無意義。反之，我們使用對數(shù)幾率回歸模型（或者對率（logit）模型），它為分配“Y屬于某個特定類”的概率而設(shè)計，范圍是 0%~100%。

數(shù)學(xué)原理是什么？

注意：這一節(jié)中的數(shù)學(xué)很有意思，但是更加技術(shù)化。如果你對高階的高年不感興趣，請盡管跳過它。

對率模型是個線性回歸的改良，通過應(yīng)用 sigmoid 函數(shù)，確保輸出 0 和 1 之間的概率。如果把它畫出來，它就像 S 型的曲線，稍后可以看到。

sigmoid 函數(shù)，它將值壓縮到 0 和 1 之間。

回憶我們的簡單線性回歸模型的原始形式，我們現(xiàn)在叫它g(X)，因為我們打算在復(fù)合函數(shù)中使用它。

現(xiàn)在，為了解決模型輸出小于 0 或者大于 1 的問題，我們打算定義一個新的函數(shù)F(g(X))，它將現(xiàn)行回歸的輸出壓縮到[0,1]區(qū)間，來轉(zhuǎn)換g(X)。你可以想到一個能這樣做的函數(shù)嗎？

你想到了 sigmoid 函數(shù)嗎？太棒了，這就對了！

所以我們將g(x)插入 sigmoid 函數(shù)中，得到了原始函數(shù)的一個函數(shù)（對，事情變得高階了），它輸出 0 和 1 之間的概率。

換句話說，我們正在計算“訓(xùn)練樣本屬于特定類”的概率：P(Y=1)。

這里我們分離了p，它是Y=1的概率，在等式左邊。如果我們打算求解等式右邊的，非常整潔的β0 + β1x + ?，以便我們能夠直接解釋我們習(xí)得的beta參數(shù)，我們會得到對數(shù)幾率比值，簡稱對率，它在左邊。這就是“對率模型”的由來。

對數(shù)幾率比值僅僅是概率比值p/(1-p)的自然對數(shù)，它會出現(xiàn)在我們每天的對話中。

在這一季的“權(quán)力的游戲”中，你認(rèn)為小惡魔掛掉的幾率有多大？

嗯...掛掉的可能性是不掛掉的兩倍。幾率是 2 比 1。的確，他太重要，不會被殺，但是我們都看到了他們對 Ned Stark 做的事情...

要注意在對率模型中，β1表示當(dāng)X變化時，對率的變化比例。換句話說，它是對率的斜率，并不是概率的斜率。

對率可能有點不直觀，但是值得理解，因為當(dāng)你解釋執(zhí)行分類任務(wù)的神經(jīng)網(wǎng)絡(luò)的輸出時，它會再次出現(xiàn)。

使用對率回歸模型的輸出來做決策

對率回歸模型的輸出，就像 S 型曲線，基于X的值展示了P(Y=1)。

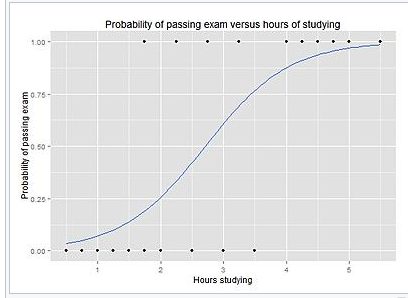
為了預(yù)測Y標(biāo)簽，是不是垃圾郵件，有沒有癌癥，是不是騙子，以及其他，你需要（為正的結(jié)果）設(shè)置一個概率截斷值，或者叫閾值（不是）。例如，如果模型認(rèn)為，郵件是垃圾郵件的概率高于 70%，就將其標(biāo)為垃圾。否則就不是垃圾。

這個閾值取決于你對假陽性（誤報）和假陰性（漏報）的容忍度。如果你在診斷癌癥，你對假陰性有極低的容忍度，因為如果病人有極小的幾率得癌癥，你都需要進(jìn)一步的測試來確認(rèn)。所以你需要為正向結(jié)果設(shè)置一個很低的閾值。

另一方面，在欺詐性貸款申請的例子中，假陽性的容忍度更高，也別是對于小額貸款，因為進(jìn)一步的審查開銷很大，并且小額貸款不值得額外的操作成本，以及對于非欺騙性的申請者來說是個障礙，它們正在等待進(jìn)一步的處理。

對數(shù)幾率回歸的最小損失

就像線性回歸的例子那樣，我們使用梯度下降來習(xí)得使損失最小的beta參數(shù)。

在對率回歸中，成本函數(shù)是這樣的度量，當(dāng)真實答案是0時，你有多么經(jīng)常將其預(yù)測為 1，或者反過來。下面是正則化的成本函數(shù)，就像我們對線性回歸所做的那樣。

當(dāng)你看到像這樣的長式子時，不要驚慌。將其拆成小部分，并從概念上思考每個部分都是什么。之后就能理解了。

第一個部分是數(shù)據(jù)損失，也就是，模型預(yù)測值和實際值之間有多少差異。第二個部分就是正則損失，也就是，我們以什么程度，懲罰模型的較大參數(shù)，它過于看重特定的特征（要記得，這可以阻止過擬合）。

我們使用低度下降，使損失函數(shù)最小，就是像上面這樣。我們構(gòu)建了一個對數(shù)幾率回歸模型，來盡可能準(zhǔn)確地預(yù)測分類。

支持向量機(jī)

我們再次位于一個充滿彈球的房間里。為什么我們總是在充滿彈球的房間里呢？我可以發(fā)誓我已經(jīng)把它們丟掉了。

SVM 是我們涉及的最后一個參數(shù)化模型。它通常與對率回歸解決相同的問題，二元分類，并產(chǎn)生相似的效果。它值得理解，因為算法本質(zhì)上是由幾何驅(qū)動的，并不是由概率思維驅(qū)動的。

SVM 可解決的一些問題示例：

• 這個圖片是貓還是狗？
• 這個評論是正面還是負(fù)面的？
• 二維圖片上的點是紅色還是藍(lán)色？

我們使用第三個例子，來展示 SVM 的工作方式。像這樣的問題叫做玩具問題，因為它們不是真實的。但是沒有東西是真實的，所以也沒關(guān)系。

這個例子中，我們的二維空間中有一些點，它們是紅色或者藍(lán)色的，并且我們打算將二者干凈地分開。

訓(xùn)練集畫在了上面的圖片中。我們打算在這個平面上劃分新的未分類的點。為了實現(xiàn)它，SVM 使用分隔直線（在高維里面是個多維的超平面），將空間分成紅色區(qū)域和藍(lán)色區(qū)域。你可以想象，分隔直線在上面的圖里面是什么樣。

具體一些，我們?nèi)绾芜x取畫這條線的位置？

下面是這條直線的兩個示例：

這些圖表使用 MicrosoftPaint 制作，在不可思議的 32 年之后，它在幾個星期之前廢棄了。R.I.P Paint :(

我希望你擁有一種直覺，覺得第一條線更好。直線到每一邊的最近的點的距離叫做間距，而 SVM 嘗試使間距最大。你可以將其看做安全空間：空間越大，嘈雜的點就越不可能被錯誤分類。

基于這個簡單的解釋，一個巨大的問題來了。

(1) 背后的數(shù)學(xué)原理是什么？

我們打算尋找最優(yōu)超平面（在我們的二維示例中是直線）。這個超平面需要（1）干凈地分隔數(shù)據(jù)，將藍(lán)色的點分到一邊，紅色的點分到另一邊，以及（2）使間距最大。這是個最優(yōu)化問題。按照（2）的需求使間距最大的時候，解需要遵循約束（1）。

求解這個問題的人類版本，就是拿一個尺子，嘗試不同的直線來分隔所有點，直到你得到了使間距最大的那條。

人們發(fā)現(xiàn)，存在求解這個最大化的數(shù)學(xué)方式，但是它超出了我們的范圍。為了進(jìn)一步解釋它，這里是個視頻講義，使用拉格朗日優(yōu)化展示了它的工作原理。

你最后求解的超平面的定義，有關(guān)它相對于特定x_i的位置，它們就叫做支持向量，并且它們通常是最接近超平面的點。

(2) 如果你不能干凈地分隔數(shù)據(jù)，會發(fā)生什么？

處理這個問題有兩個方式。

2.1 軟化“分隔”的定義

我們允許一些錯誤，也就是我們允許紅色區(qū)域里面有一些藍(lán)色點，或者藍(lán)色區(qū)域里有一些紅色點。我們向損失函數(shù)中。為錯誤分類的樣本添加成本C來實現(xiàn)。基本上我們說，錯誤分類是可以接受的，只是會產(chǎn)生一些成本。

2.2 將數(shù)據(jù)放到高維

我們可以創(chuàng)建非線性的分類器，通過增加維數(shù)，也就是，包含x^2，x^3，甚至是cos(x)，以及其它。突然，你就有了一個邊界，當(dāng)我們將其帶回低維表示時，它看起來有些彎曲。

本質(zhì)上，這就類似紅的和藍(lán)色的彈球都在地面上，它們不能用一條直線分隔。但是如果你讓所有紅色的彈球離開地面，像右圖這樣，你就能畫一個平面來分隔它們。之后你讓他們落回地面，就知道了藍(lán)色和紅色的邊界。

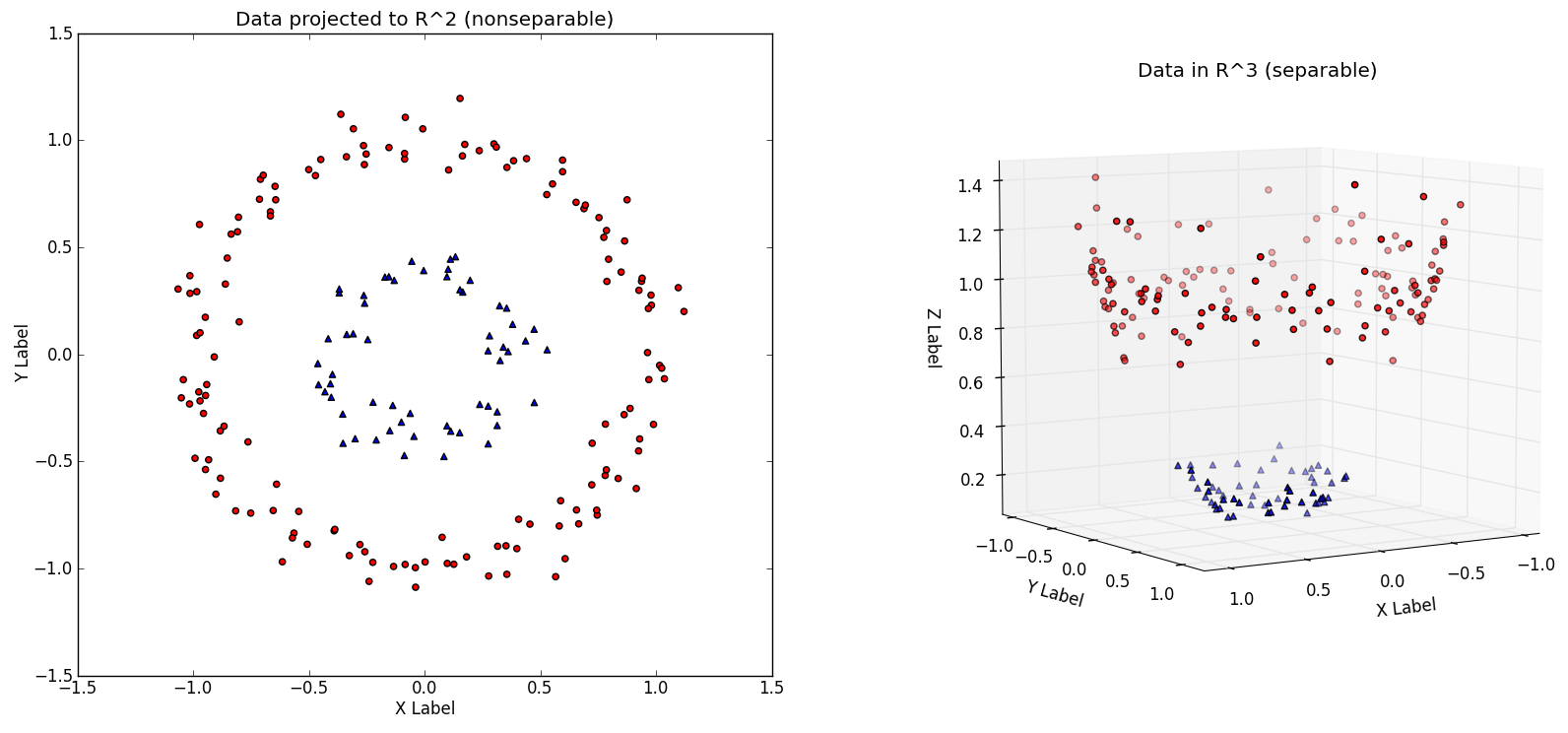
二維空間R^2中的非線性可分的數(shù)據(jù)集，以及映射到高維的相同數(shù)據(jù)集，第三個維度是x^2+y^2（來源：http://www.eric-kim.net/eric-kim-net/posts/1/kernel_trick.html）

決策邊界展示為綠色，左邊是三維空間，右邊是二維空間。與上一張來源相同。

總之，SVM 用于二元分類。它們嘗試尋找一個平面，干凈地分隔兩個類。如果這不可能，我們可以軟化“分隔”的定義，或者我們把數(shù)據(jù)放到高維，以便我們可以干凈地分隔數(shù)據(jù)。

好的！

這一節(jié)中我們涉及了：

• 監(jiān)督學(xué)習(xí)的分類任務(wù)
• 兩種基礎(chǔ)的分類方法：對數(shù)幾率回歸（LR）和支持向量機(jī)（SVM）
• 常見概念：sigmoid 函數(shù)，對數(shù)幾率（對率），以及假陽性（誤報）和假陰性（漏報）

在“2.3：監(jiān)督學(xué)習(xí) III”中，我們會深入非參數(shù)化監(jiān)督學(xué)習(xí)，其中算法背后的概念都非常直觀，并且對于特定類型的問題，表現(xiàn)都很優(yōu)秀，但是模型可能難以解釋。

練習(xí)材料和擴(kuò)展閱讀

2.2a 對數(shù)幾率回歸

Data School 擁有一個對數(shù)幾率回歸的非常棒的深入指南。我們也繼續(xù)向你推薦《An Introduction to Statistical Learning》。對數(shù)幾率回歸請見第四章，支持向量機(jī)請見第九章。

為了解釋對數(shù)幾率回歸，我們推薦你處理這個問題集。你需要注冊站點來完成它。很不幸，這就是人生。

2.2b 深入 SVM

為了深入 SVM 背后的數(shù)學(xué)，在 MIT 6.034：人工智能課程中觀看 Patrick Winston 教授的講義，并查看這個教程來完成 Python 實現(xiàn)。