這篇博客介紹RNN基礎(chǔ)。

具體關(guān)于RNN的細(xì)節(jié)介紹和實(shí)現(xiàn)，推薦wildml的這個(gè)系列博客，一共四篇，帶你由淺入深學(xué)習(xí)RNN和Theano實(shí)現(xiàn)。補(bǔ)充：看到知乎上有人把這個(gè)系列翻譯出來了，可以看看。

另外，Karpathy（char-rnn的作者）的博客講了更多關(guān)于RNN和語言模型的知識。

這里我簡單總結(jié)下。

1. RNN

這里說的RNN特指循環(huán)神經(jīng)網(wǎng)絡(luò)（Recurrent Neural Network），先看下面這張圖：

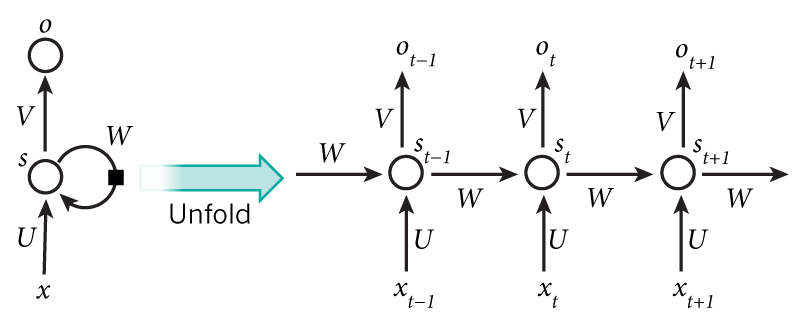
簡單介紹下符號：

先看左邊沒有展開的圖，若輸入x直接到輸出o，那就是一個(gè)普通的神經(jīng)元；RNN就是在原來的基礎(chǔ)上，增加了一個(gè)中間狀態(tài)s，然后這個(gè)中間狀態(tài)會(huì)受到上一個(gè)時(shí)間點(diǎn)（序列中前一個(gè)）中間狀態(tài)的影響。

按時(shí)間展開這個(gè)RNN單元，就可以獲得右邊的圖，U，V，W是唯一的。

用數(shù)學(xué)語言描述上面的圖：

下面給出theano實(shí)現(xiàn)：

# 1.先定義單個(gè)時(shí)間序列下的計(jì)算規(guī)則
def forward_prop_step(x_t, s_t_prev, U, V, W):
    s_t = T.tanh(U[:, x_t] + W.dot(s_t_prev))
    o_t = T.nnet.softmax(V.dot(s_t))
    return [o_t[0], s_t]
# 2.對輸入序列x，計(jì)算隱藏狀態(tài)序列s，和輸出序列o；thean中的scan相當(dāng)于for循環(huán)。
[o, s], updates = theano.scan(
    forward_prop_step,
    sequences=x,
    outputs_info=[None, dict(initial=T.zeros(self.hidden_dim))],
    non_sequences=[U, V, W],
    truncate_gradient=self.bptt_truncate,
    strict=True)

預(yù)測和損失函數(shù)：

prediction = T.argmax(o, axis=1)
o_error = T.sum(T.nnet.categorical_crossentropy(o, y))

2. GRU（門限遞歸單元）

普通的RNN會(huì)有梯度消失的問題，即對于較長的輸入序列，會(huì)出現(xiàn)梯度為0的狀況。

于是產(chǎn)生了GRU（門限遞歸單元）和LSTM（長短項(xiàng)記憶）。

GRU：

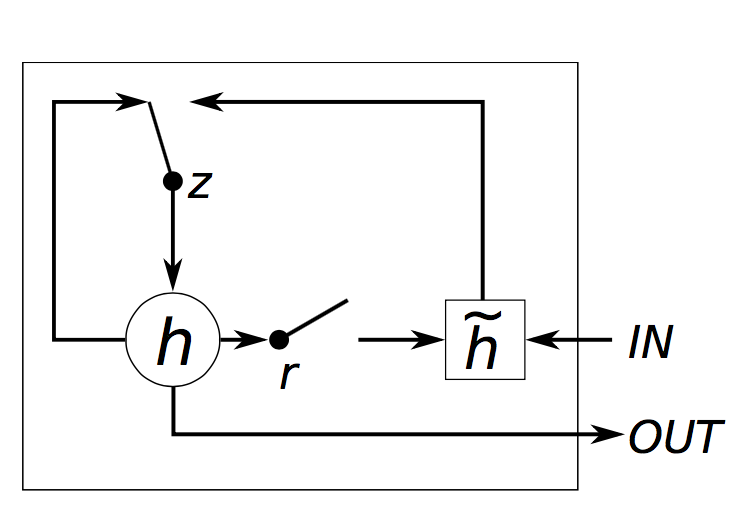
解釋：

Theano實(shí)現(xiàn)：

# 獲得embedding
x_e = E[:, x_t]

# GRU 
z_t = T.nnet.hard_sigmoid(U[0].dot(x_e) + W[0].dot(s_t_prev) + b[0])
r_t = T.nnet.hard_sigmoid(U[1].dot(x_e) + W[1].dot(s_t_prev) + b[1])
h_t = T.tanh(U[2].dot(x_e) + W[2].dot(s_t_prev * r_t) + b[2])
s_t = (T.ones_like(z_t) - z_t) * h_t + z_t * s_t_prev

3. LSTM（長短項(xiàng)記憶）

繼續(xù)介紹LSTM：

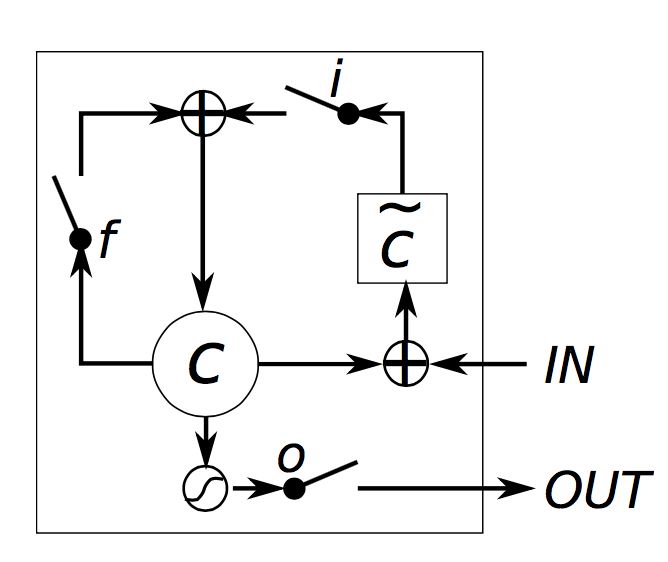
解釋：

Tensorflow實(shí)現(xiàn)：

參數(shù)定義：

# Parameters:
  # Input gate: input, previous output, and bias.
  ix = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  im = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  ib = tf.Variable(tf.zeros([1, num_nodes]))
  # Forget gate: input, previous output, and bias.
  fx = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  fm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  fb = tf.Variable(tf.zeros([1, num_nodes]))
  # Memory cell: input, state and bias.                             
  cx = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  cm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  cb = tf.Variable(tf.zeros([1, num_nodes]))
  # Output gate: input, previous output, and bias.
  ox = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  om = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  ob = tf.Variable(tf.zeros([1, num_nodes]))
  # Variables saving state across unrollings.
  saved_output = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
  saved_state = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
  # Classifier weights and biases.
  w = tf.Variable(tf.truncated_normal([num_nodes, vocabulary_size], -0.1, 0.1))
  b = tf.Variable(tf.zeros([vocabulary_size]))

計(jì)算規(guī)則：

def lstm_cell(i, o, state):
    """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
    Note that in this formulation, we omit the various connections between the
    previous state and the gates."""
    input_gate = tf.sigmoid(tf.matmul(i, ix) + tf.matmul(o, im) + ib)
    forget_gate = tf.sigmoid(tf.matmul(i, fx) + tf.matmul(o, fm) + fb)
    update = tf.matmul(i, cx) + tf.matmul(o, cm) + cb
    state = forget_gate * state + input_gate * tf.tanh(update)
    output_gate = tf.sigmoid(tf.matmul(i, ox) + tf.matmul(o, om) + ob)
    return output_gate * tf.tanh(state), state

4. 一些細(xì)節(jié)

?
符號°代表矩陣的Element-wise product，也稱為Hadamard product。
?
在theano和tensorflow中，*直接表示Element-wise product。
?
而theano中的.dot和tensorflow中的tf.matmul，表示矩陣乘法。