轉自：http://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html
沒有仔細看，先留著，有空在手機上再看
在做分類時常常需要估算不同樣本之間的相似性度量(Similarity Measurement)，這時通常采用的方法就是計算樣本間的“距離”(Distance)。采用什么樣的方法計算距離是很講究，甚至關系到分類的正確與否。
本文的目的就是對常用的相似性度量作一個總結。
本文目錄：
歐氏距離
曼哈頓距離
切比雪夫距離
閔可夫斯基距離
標準化歐氏距離
馬氏距離
夾角余弦
漢明距離
杰卡德距離 & 杰卡德相似系數
相關系數 & 相關距離
信息熵
歐氏距離(Euclidean Distance)
歐氏距離是最易于理解的一種距離計算方法，源自歐氏空間中兩點間的距離公式。
(1)二維平面上兩點a(x1,y1)與b(x2,y2)間的歐氏距離：
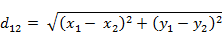
(2)三維空間兩點a(x1,y1,z1)與b(x2,y2,z2)間的歐氏距離：
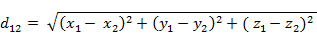
(3)兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的歐氏距離：
也可以用表示成向量運算的形式：
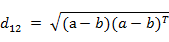
(4)Matlab計算歐氏距離
Matlab計算距離主要使用pdist函數。若X是一個M×N的矩陣，則pdist(X)將X矩陣M行的每一行作為一個N維向量，然后計算這M個向量兩兩間的距離。
例子：計算向量(0,0)、(1,0)、(0,2)兩兩間的歐式距離
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'euclidean')
結果：
D = 1.0000 2.0000 2.2361
曼哈頓距離(Manhattan Distance)
從名字就可以猜出這種距離的計算方法了。想象你在曼哈頓要從一個十字路口開車到另外一個十字路口，駕駛距離是兩點間的直線距離嗎？顯然不是，除非你能穿越大樓。實際駕駛距離就是這個“曼哈頓距離”。而這也是曼哈頓距離名稱的來源， 曼哈頓距離也稱為城市街區距離(City Block distance)。
(1)二維平面兩點a(x1,y1)與b(x2,y2)間的曼哈頓距離
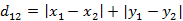
(2)兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的曼哈頓距離
(3) Matlab計算曼哈頓距離
例子：計算向量(0,0)、(1,0)、(0,2)兩兩間的曼哈頓距離
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'cityblock')
結果：
D = 1 2 3
切比雪夫距離 ( Chebyshev Distance )
國際象棋玩過么？國王走一步能夠移動到相鄰的8個方格中的任意一個。那么國王從格子(x1,y1)走到格子(x2,y2)最少需要多少步？自己走走試試。你會發現最少步數總是max( | x2-x1 | , | y2-y1 | ) 步 。有一種類似的一種距離度量方法叫切比雪夫距離。
(1)二維平面兩點a(x1,y1)與b(x2,y2)間的切比雪夫距離
(2)兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的切比雪夫距離
這個公式的另一種等價形式是
看不出兩個公式是等價的？提示一下：試試用放縮法和夾逼法則來證明。
(3)Matlab計算切比雪夫距離
例子：計算向量(0,0)、(1,0)、(0,2)兩兩間的切比雪夫距離
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'chebychev')
結果：
D = 1 2 2
閔可夫斯基距離(Minkowski Distance)
閔氏距離不是一種距離，而是一組距離的定義。
(1) 閔氏距離的定義
兩個n維變量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的閔可夫斯基距離定義為：
其中p是一個變參數。
當p=1時，就是曼哈頓距離
當p=2時，就是歐氏距離
當p→∞時，就是切比雪夫距離
根據變參數的不同，閔氏距離可以表示一類的距離。
(2)閔氏距離的缺點
閔氏距離，包括曼哈頓距離、歐氏距離和切比雪夫距離都存在明顯的缺點。
舉個例子：二維樣本(身高,體重)，其中身高范圍是150190，體重范圍是5060，有三個樣本：a(180,50)，b(190,50)，c(180,60)。那么a與b之間的閔氏距離（無論是曼哈頓距離、歐氏距離或切比雪夫距離）等于a與c之間的閔氏距離，但是身高的10cm真的等價于體重的10kg么？因此用閔氏距離來衡量這些樣本間的相似度很有問題。
簡單說來，閔氏距離的缺點主要有兩個：(1)將各個分量的量綱(scale)，也就是“單位”當作相同的看待了。(2)沒有考慮各個分量的分布（期望，方差等)可能是不同的。
(3)Matlab計算閔氏距離
例子：計算向量(0,0)、(1,0)、(0,2)兩兩間的閔氏距離（以變參數為2的歐氏距離為例）
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'minkowski',2)
結果：
D = 1.0000 2.0000 2.2361
標準化歐氏距離 (Standardized Euclidean distance )
(1)標準歐氏距離的定義
標準化歐氏距離是針對簡單歐氏距離的缺點而作的一種改進方案。標準歐氏距離的思路：既然數據各維分量的分布不一樣，好吧！那我先將各個分量都“標準化”到均值、方差相等吧。均值和方差標準化到多少呢？這里先復習點統計學知識吧，假設樣本集X的均值(mean)為m，標準差(standard deviation)為s，那么X的“標準化變量”表示為：
而且標準化變量的數學期望為0，方差為1。因此樣本集的標準化過程(standardization)用公式描述就是：
標準化后的值 = ( 標準化前的值 － 分量的均值 ) /分量的標準差
經過簡單的推導就可以得到兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的標準化歐氏距離的公式：
如果將方差的倒數看成是一個權重，這個公式可以看成是一種加權歐氏距離(Weighted Euclidean distance)。
(2)Matlab計算標準化歐氏距離
例子：計算向量(0,0)、(1,0)、(0,2)兩兩間的標準化歐氏距離 (假設兩個分量的標準差分別為0.5和1)
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'seuclidean',[0.5,1])
結果：
D = 2.0000 2.0000 2.8284
馬氏距離(Mahalanobis Distance)
（1）馬氏距離定義
有M個樣本向量X1~Xm，協方差矩陣記為S，均值記為向量μ，則其中樣本向量X到u的馬氏距離表示為：
而其中向量Xi與Xj之間的馬氏距離定義為：
若協方差矩陣是單位矩陣（各個樣本向量之間獨立同分布）,則公式就成了：
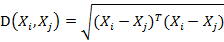
也就是歐氏距離了。
若協方差矩陣是對角矩陣，公式變成了標準化歐氏距離。
(2)馬氏距離的優缺點：量綱無關，排除變量之間的相關性的干擾。
(3) Matlab計算(1 2)，( 1 3)，( 2 2)，( 3 1)兩兩之間的馬氏距離
X = [1 2; 1 3; 2 2; 3 1]
Y = pdist(X,'mahalanobis')
結果：
Y = 2.3452 2.0000 2.3452 1.2247 2.4495 1.2247
夾角余弦(Cosine)
有沒有搞錯，又不是學幾何，怎么扯到夾角余弦了？各位看官稍安勿躁。幾何中夾角余弦可用來衡量兩個向量方向的差異，機器學習中借用這一概念來衡量樣本向量之間的差異。
(1)在二維空間中向量A(x1,y1)與向量B(x2,y2)的夾角余弦公式：
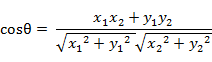
(2) 兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夾角余弦
類似的，對于兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)，可以使用類似于夾角余弦的概念來衡量它們間的相似程度。
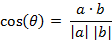
即：
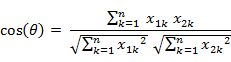
夾角余弦取值范圍為[-1,1]。夾角余弦越大表示兩個向量的夾角越小，夾角余弦越小表示兩向量的夾角越大。當兩個向量的方向重合時夾角余弦取最大值1，當兩個向量的方向完全相反夾角余弦取最小值-1。
夾角余弦的具體應用可以參閱參考文獻[1]。
(3)Matlab計算夾角余弦
例子：計算(1,0)、( 1,1.732)、( -1,0)兩兩間的夾角余弦
X = [1 0 ; 1 1.732 ; -1 0]
D = 1- pdist(X, 'cosine') % Matlab中的pdist(X, 'cosine')得到的是1減夾角余弦的值
結果：
D = 0.5000 -1.0000 -0.5000
漢明距離(Hamming distance)
(1)漢明距離的定義
兩個等長字符串s1與s2之間的漢明距離定義為將其中一個變為另外一個所需要作的最小替換次數。例如字符串“1111”與“1001”之間的漢明距離為2。
應用：信息編碼（為了增強容錯性，應使得編碼間的最小漢明距離盡可能大）。
(2)Matlab計算漢明距離
Matlab中2個向量之間的漢明距離的定義為2個向量不同的分量所占的百分比。
例子：計算向量(0,0)、(1,0)、(0,2)兩兩間的漢明距離
X = [0 0 ; 1 0 ; 0 2];
D = PDIST(X, 'hamming')
結果：
D = 0.5000 0.5000 1.0000
杰卡德相似系數(Jaccard similarity coefficient)
(1) 杰卡德相似系數
兩個集合A和B的交集元素在A，B的并集中所占的比例，稱為兩個集合的杰卡德相似系數，用符號J(A,B)表示。
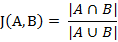
杰卡德相似系數是衡量兩個集合的相似度一種指標。
(2) 杰卡德距離
與杰卡德相似系數相反的概念是杰卡德距離(Jaccard distance)。杰卡德距離可用如下公式表示：
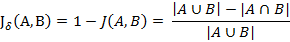
杰卡德距離用兩個集合中不同元素占所有元素的比例來衡量兩個集合的區分度。
(3) 杰卡德相似系數與杰卡德距離的應用
可將杰卡德相似系數用在衡量樣本的相似度上。
樣本A與樣本B是兩個n維向量，而且所有維度的取值都是0或1。例如：A(0111)和B(1011)。我們將樣本看成是一個集合，1表示集合包含該元素，0表示集合不包含該元素。
p ：樣本A與B都是1的維度的個數
q ：樣本A是1，樣本B是0的維度的個數
r ：樣本A是0，樣本B是1的維度的個數
s ：樣本A與B都是0的維度的個數
那么樣本A與B的杰卡德相似系數可以表示為：
這里p+q+r可理解為A與B的并集的元素個數，而p是A與B的交集的元素個數。
而樣本A與B的杰卡德距離表示為：
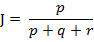
(4)Matlab 計算杰卡德距離
Matlab的pdist函數定義的杰卡德距離跟我這里的定義有一些差別，Matlab中將其定義為不同的維度的個數占“非全零維度”的比例。
例子：計算(1,1,0)、(1,-1,0)、(-1,1,0)兩兩之間的杰卡德距離
X = [1 1 0; 1 -1 0; -1 1 0]
D = pdist( X , 'jaccard')
結果
D =0.5000 0.5000 1.0000
相關系數 ( Correlation coefficient )與相關距離(Correlation distance)
(1) 相關系數的定義
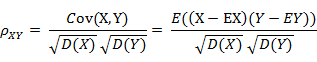
相關系數是衡量隨機變量X與Y相關程度的一種方法，相關系數的取值范圍是[-1,1]。相關系數的絕對值越大，則表明X與Y相關度越高。當X與Y線性相關時，相關系數取值為1（正線性相關）或-1（負線性相關）。
(2)相關距離的定義
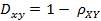
(3)Matlab計算(1, 2 ,3 ,4 )與( 3 ,8 ,7 ,6 )之間的相關系數與相關距離
X = [1 2 3 4 ; 3 8 7 6]
C = corrcoef( X' ) %將返回相關系數矩陣
D = pdist( X , 'correlation')
結果：
C =
1.0000 0.4781
0.4781 1.0000
D =0.5219
其中0.4781就是相關系數，0.5219是相關距離。
信息熵(Information Entropy)
信息熵并不屬于一種相似性度量。那為什么放在這篇文章中啊？這個。。。我也不知道。 (╯▽╰)
信息熵是衡量分布的混亂程度或分散程度的一種度量。分布越分散(或者說分布越平均)，信息熵就越大。分布越有序（或者說分布越集中），信息熵就越小。
計算給定的樣本集X的信息熵的公式：
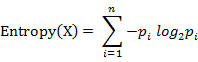
參數的含義：
n：樣本集X的分類數
pi：X中第i類元素出現的概率
信息熵越大表明樣本集S分類越分散，信息熵越小則表明樣本集X分類越集中。。當S中n個分類出現的概率一樣大時（都是1/n），信息熵取最大值log2(n)。當X只有一個分類時，信息熵取最小值0
參考資料：
[1]吳軍. 數學之美 系列 12 - 余弦定理和新聞的分類.
http://www.google.com.hk/ggblog/googlechinablog/2006/07/12_4010.html
[2] Wikipedia. Jaccard index.
http://en.wikipedia.org/wiki/Jaccard_index
[3] Wikipedia. Hamming distance
http://en.wikipedia.org/wiki/Hamming_distance
[4] 求馬氏距離（Mahalanobis distance ）matlab版
http://junjun0595.blog.163.com/blog/static/969561420100633351210/
[5] Pearson product-moment correlation coefficient
http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient
